Once again consider an arbitrary body in equilibrium and pass a section through the body as shown in Figure 1. Let the section be perpendicular to the x-axis.
 |
 |
| (a) | (b) Internal forces on the cross section |
Figure 1(a,b)
Consider an infinitesimally small area \(\Delta A_x\) surrounding point \(Q\) on the section as in Figure 2. We use the subscript \(x\) for \(\Delta A_x\) to indicate the \(x\) axis is perpendicular to this area. A finite small force vector \(\Delta {\bf F}\) arising from the action of the other part of the body, acts on \(\Delta A_x\). Let’s resolve \(\Delta{\bf F}\) into its components along the \(x\), \(y\), and \(z\) axes: \[ \Delta {\bf F}=\Delta F_x {\bf i}+\Delta F_y {\bf j}+\Delta F_z {\bf k} \]
To find the intensity of the internal force at \(Q\) (or particularly the stress components), we divide the components of \(\Delta{\bf F}\) by the area and let \(\Delta A_x\) approach zero \[ \begin{align} \tau_{xx}=\lim_{\Delta A_x\to 0}\frac{\Delta F_x}{\Delta A_x}\\ \tau_{xy}=\lim_{\Delta A_x\to 0}\frac{\Delta F_y}{\Delta A_x}\\ \tau_{xz}=\lim_{\Delta A_x\to 0}\frac{\Delta F_z}{\Delta A_x}\\ \end{align} \]
The first subscript signifies that the plane is perpendicular to the x-axis and the second subscript indicates the direction of the component of the force.
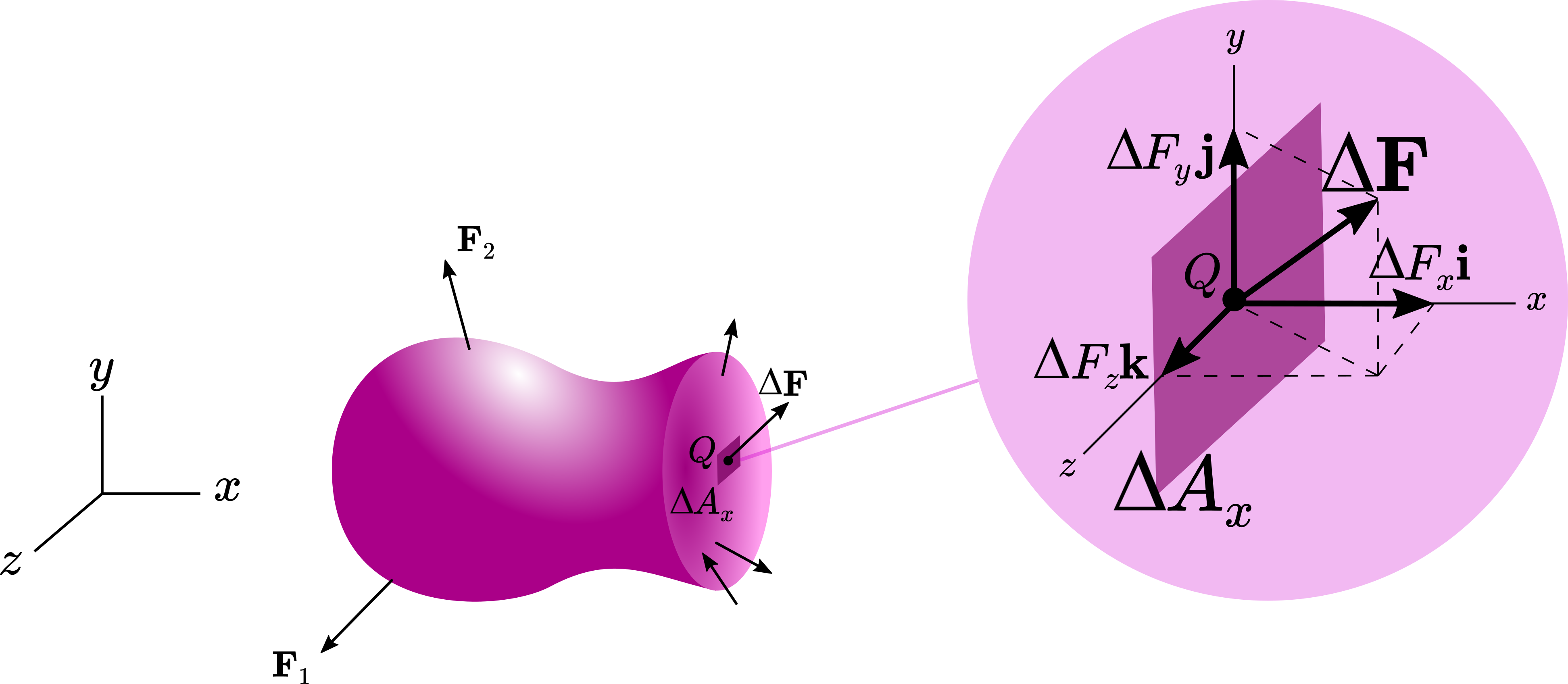 |
| Figure 2 |
Note that \(\Delta A_x\to 0\) is in contradiction with the fact that materials are composed of atoms and molecules, but keep in mind that We can repeat what we did to define \(\tau_{xx}\) and \(\tau_{xy}\) , to define 6 other components of stress at Q. That is, we consider a plane that crosses Q and is perpendicular to the y axes and an incremental area \(\Delta A_y\) around Q on this plane (Figure 3). Then we find the incremental force \(\Delta {\bf F’}\) that acts on \(\Delta A_y\) , we can define three more components of stress at Q \[ \begin{align} \tau_{yx}=\lim_{\Delta A_y\to 0}\frac{\Delta F’_x}{\Delta A_y}\\ \tau_{yy}=\lim_{\Delta A_y\to 0}\frac{\Delta F’_y}{\Delta A_y}\\ \tau_{yz}=\lim_{\Delta A_y\to 0}\frac{\Delta F’_z}{\Delta A_y}\\ \end{align} \] where \(\Delta{\bf F’}=\Delta F’_x{\bf i}+\Delta F’_y {\bf j}+\Delta F’_z{\bf k}\). Again \(\tau_{yy}\) is the normal stress because \(\Delta F’_y {\bf j}\) is normal to \(\Delta A_y\) and hence we can denote \(\tau_{yy}\) by \(\sigma_y\). The other two components \(\tau_{yx}\) and \(\tau_{yz}\) are shear stresses. In a similar manner, we can define, \(\tau_{zx}, \tau_{zy}\), and \(\tau_{zz}\) (also denoted by \(\sigma_z\)). Therefore, stress at a point has 9 components: 3 normal components \(\sigma_x, \sigma_y\) and \(\sigma_z\) and 6 shear components \(\tau_{xy},\tau_{xz},\tau_{yx},\tau_{yz},\tau_{zx}\) and \(\tau_{zy}\) (Figure 4). These 9 components specify the state of stress acting around a point in a body.Read more about ∆Ax → 0
Collapse the explanation
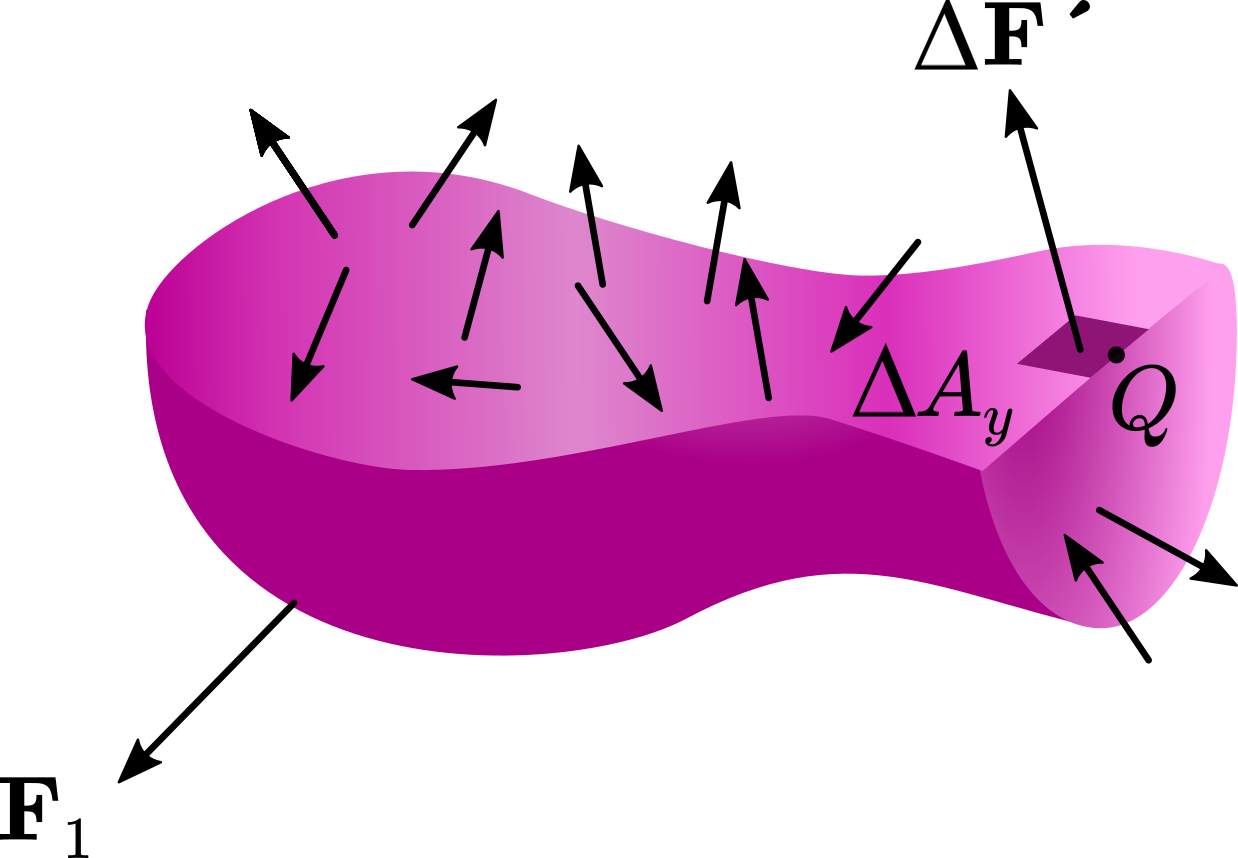
Figure 3
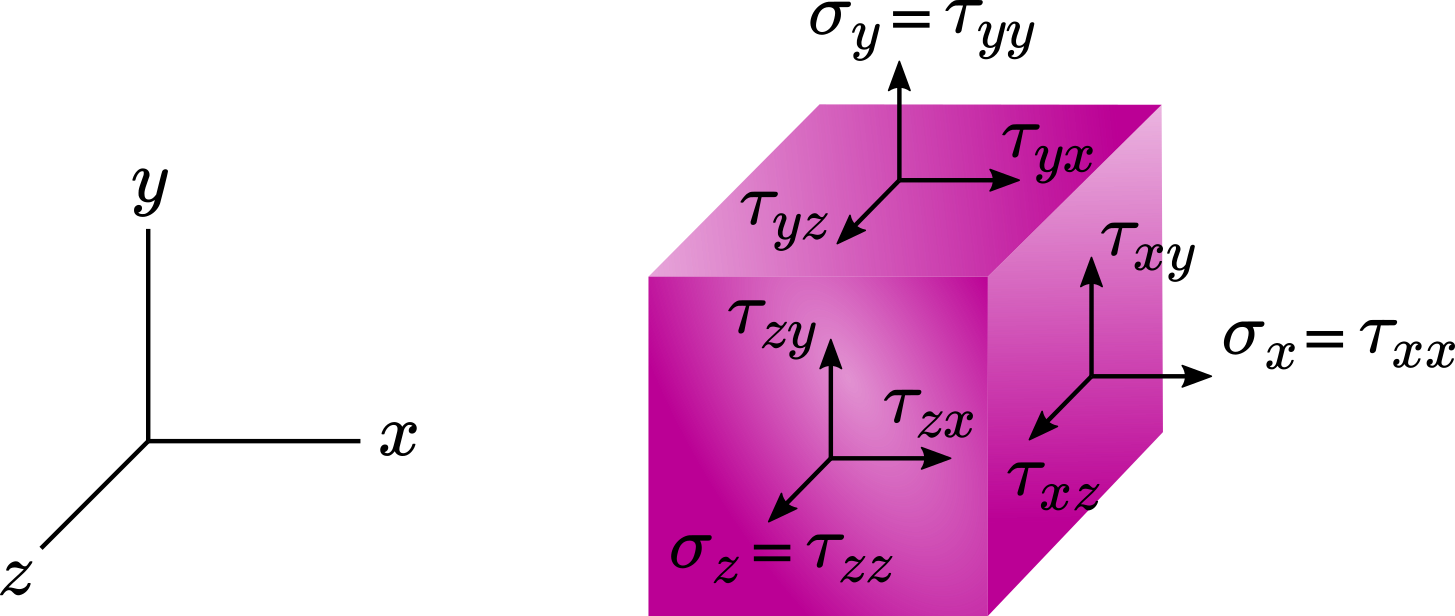
Figure 4
Obviously we can choose any three mutually perpendicular axes as our coordinate system. If we know the state of stress (the 9 components of stress) at a point in one coordinate system, then we can find the components of stress at that point on any arbitrary plane or in general, its components in any other coordinate system. In chapter 8, we will discuss how we can convert the components of stress in a given coordinate system to a new coordinate system. We can arrange the nine stress components in a matrix form \[ \begin{bmatrix}{\tau_{x x}} & {\tau_{x y}} & {\tau_{x z}} \\{\tau _{y x}} & {\tau _{y y}} & {\tau _{y z}} \\{\tau _{z x}} & {\tau _{z y}} & {\tau _{z z}}\end{bmatrix}\equiv\begin{bmatrix}{\sigma_{x}} & {\tau_{x y}} & {\tau_{x z}} \\{\tau_{y x}} & {\sigma_{y}} & {\tau_{y z}} \\{\tau_{z x}} & {\tau_{z y}} & {\sigma_{z}}\end{bmatrix} \] The above arrangement is called the matrix representation of the stress state at a point (or stress tensor) . In elementary courses, you have faced two types of quantities: vectors and scalars. Stress is neither a scalar nor a vector. To denote the components of a vector we need only one index; for example, \[ {\bf F}=F_x{\bf i}+F_y {\bf j}+F_z {\bf k}=\begin{bmatrix} F_x\\ F_y\\ F_z \end{bmatrix} \] but to identify the components of stress we need two indices. Stress is a new type of quantities called second-rank tensor. A second-rank tensor is a quantity whose components transform in a certain way discussed later under a rotation of axes. In the International System or SI: 1 Pa = 1 N/m2 In the U.S. customary system: 1 ksi = 103 psi = 103 lb/in2Read more on State of Stress
Hide
Matrix Representation
Read more on stress tensor
Collapse title
Units of stress
Stress units in the U.S. customary system
Hide stress units in the U.S. customary system
