Riemann sums
Let \(f(x)\) be defined for \(a\leq x\leq b\) (Figure 1). Assume at pleasure \(n-1\) points between \(a\) and \(b\) \[a=x_{0}<x_{1}<x_{2}<\cdots<x_{n}=b,\] thus dividing the interval \(I=[a,b]\) into \(n\) subintervals: \[[a,x_{1}],[x_{1},x_{2}],\cdots,[x_{n-1},b].\] In each of these subintervals, take a value of \(x=x_{k}^{*}\) where \(x_{k-1}\leq x_{k}^{*}\leq x_{k}\), and form the sum \[S_{n}=f(x_{1}^{*})(x_{1}-x_{0})+f(x_{2}^{*})(x_{2}-x_{1})+\cdots+f(x_{n}^{*})(x_{n}-x_{n-1})\tag{8.1.1}\] This sum is called a Riemann sum for \(f\) on the interval \([a,b]\), after German mathematician George Friedrich Bernhard Riemann (1826–1866). Now let’s see what the geometrical interpretation of \(S_{n}\) is. First suppose \(f(x)\geq0\) for all \(x\in[a,b]\). In this case
\(f(x_{1}^{*})(x_{1}-x_{0})=\) the area of the rectangle \(AP_{1}R_{1}M_{1},\)
\(f(x_{2}^{*})(x_{2}-x_{1})=\) the area of the rectangle \(M_{1}P_{2}R_{2}M_{2},\)
\(\vdots\)
\(f(x_{n-1}^{*})(x_{n-1}-x_{n-2})=\) the area of the rectangle \(M_{n-2}P_{n-1}R_{n-1}M_{n-1}\),
\(f(x_{n}^{*})(x_{n}-x_{n-1})=\) the area of the rectangle \(M_{n-1}P_{n}R_{n}B\).
Thus \(S_{n}\) represents the total area of all rectangles in Figure 1, and approximates the area of the region that lies between the curve \(y=f(x)\) and the \(x\)-axis between \(x=a\) and \(x=b\).
If \(f(x)\) takes both positive and negative values on \([a,b]\), then \(S_{n}\) is an approximation for the net signed area; that is, the area below the curve \(y=f(x)\) and above the \(x\)-axis minus the area above the curve \(y=f(x)\) and below the \(x\)-axis from \(x=a\) to \(x=b\), as suggested in Figure 2.
The Riemann sum is often shortened as \[S_{n}=\sum_{k=1}^{n}f(x_{k}^{*})(x_{k}-x_{k-1}),\] where \(\Sigma\) (sigma), Greek form of the letter \(S\), stands for the word “summation.” The whole expression indicates that the sum is to be taken of all terms obtained from \(f(x_{k}^{*})(x_{k}-x_{k-1})\) by giving to \(k\) in succession the values of \(1,2,3,\dots,n\).
By introducing the symbol \[\Delta_{k}x=x_{k}-x_{k-1},\] we can shorten it further and write: \[S_{n}=\sum_{k=1}^{n}f(x_{k}^{*})\Delta_{k}x.\tag{8.1.2}\] Please note that here \(\Delta_{k}\) is not a factor, but denotes the difference (here the length of the \(k\)-th subinterval).
- Some books, write \(\Delta x_{k}\) instead of \(\Delta_{k}x\).
Read about some specific types of Riemann sums
Hide the speci
Some Specific Types of Riemann Sums
- If the sample point in each subinterval \(x_{k}^{*}\) is the left endpoint of the subinterval; that is, if \(x_{k}^{*}=x_{k-1}\) for all \(k\), then \(S_{n}\) is called a left Riemann sum (see Figure 3).
- If the sample point in each interval \(x_{k}^{*}\) is the right endpoint of the subinterval; that is, if \(x_{k}^{*}=x_{k}\) for all \(k\), then \(S_{n}\) is called a right Riemann sum (see Figure 4).
- If the sample point in each interval \(x_{k}^{*}\) is the midpoint of the subinterval; that is, if \(x_{k}^{*}=(x_{k}+x_{k-1})/2\) for all \(k\), then \(S_{n}\) is called a middle Riemann sum (see Figure 5).
- If the sample point in each interval \(x_{k}^{*}\) is chosen such that \(f(x_{k}^{*})\) is the maximum value of \(f\) on the subinterval \([x_{k-1},x_{k}]\) for all \(k\), then \(S_{n}\) is called an upper Riemann sum (see Figure 6).
- If the sample point in each interval \(x_{k}^{*}\) is chosen such that \(f(x_{k}^{*})\) is the minimum value of \(f\) on the subinterval \([x_{k-1},x_{k}]\) for all \(k\), then \(S_{n}\) is called a lower Riemann sum (see Figure 7).
Limit of the Riemann Sums as \(n\to\infty\)
As shown in Figure 8, if the number of subintervals \(n\) increases such that the subintervals lengths (or widths) get smaller and the rectangles become thinner, then the Riemann sum \(S_{n}\) will be a better approximation to the net area between the curve \(y=f(x)\) and the \(x\)-axis.
| n=11 | n=20 | n=40 |
|
 |
 |
Figure 8. As the number of subintervals $n$ increases, $S_n$ becomes a better approximation to the net area that lie between the curve $y = f(x)$ and the x-axis.
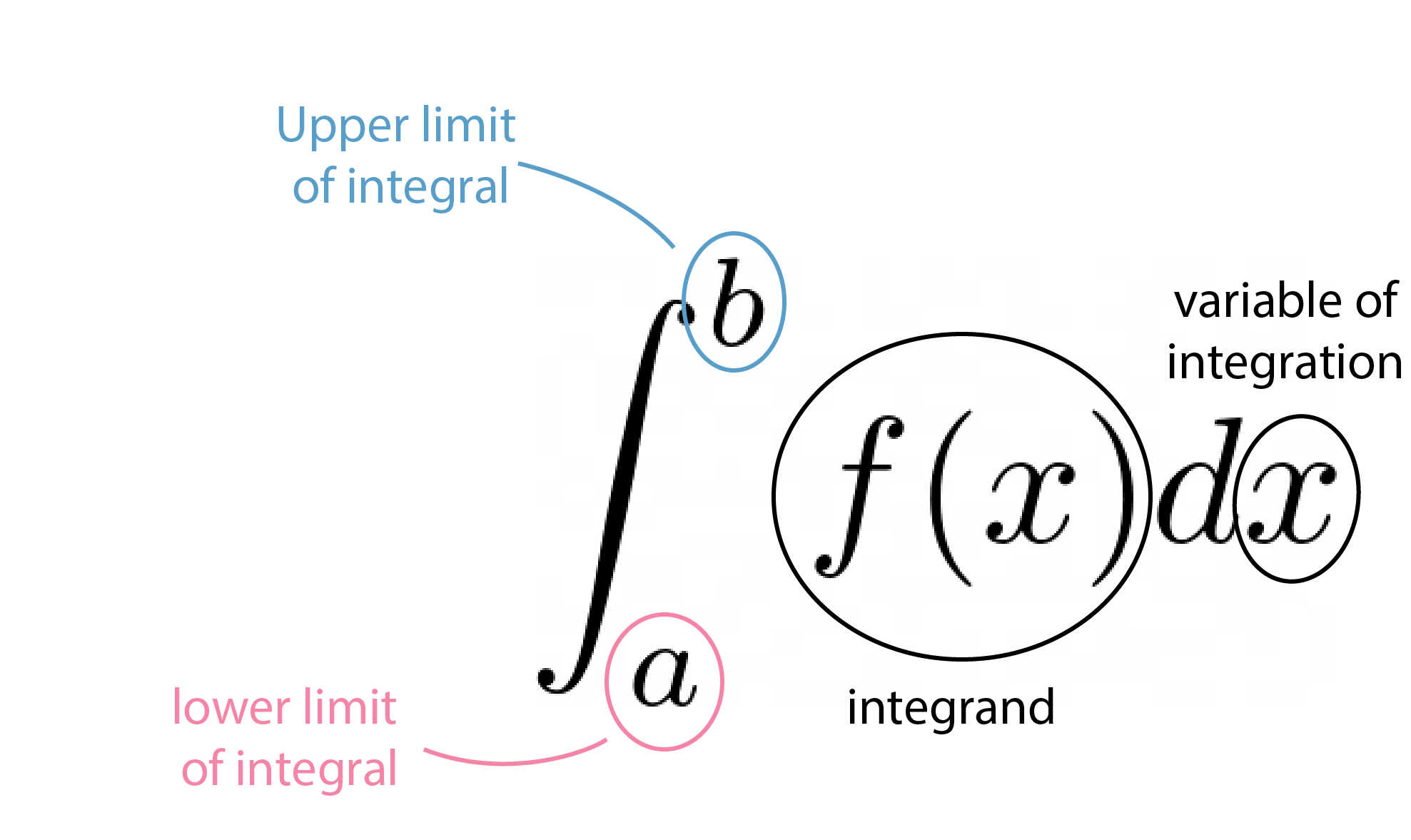
Now let the number of subintervals \(n\) increase indefinitely \((n\to\infty)\), while the width of the widest subinterval approaches zero. If the sum (8.1.1) (or (8.1.2)) approaches a number which is independent of the choice of the \(x_{k}\)’s and of the \(x_{k}^{*}\)’s, its limit is called the definite integral of \(f(x)\) between \(a\) and \(b\) and is denoted by \({\int_{a}^{b}f(x)}dx\).
We note that
- The use of the word “integral” and of the symbol \(\int\) suggests a connection with the indefinite integrals in the previous Chapter. This connection will be shown in Section on the Fundamental Theorem of Calculus.
- The symbol \(\int\) is a modified form of \(S\) (that stands for summation).
- We call \(a\) the lower limit and \(b\) the upper limit of integration (or of the internal), and the function \(f(x)\) the integrand.
- If the integral \(\int_{a}^{b}f(x)dx\) exists, \(f(x)\) is called integrable between \(a\) and \(b\).
- If \(f\) is continuous on the interval \((a,b)\) then \(\int_{a}^{b}f(x)dx\) exists. The proof of this theorem is beyond the scope of an elementary course.
The letter \(k\) chosen for the summation index in the Riemann sum \(S_{n}=\sum_{k=1}^{n}f(x_{k}^{*})\Delta_{k}x\) is a dummy variable; that is, it can be replaced by any other letter such as \(i\) without affecting the value of the sum (provided, of course, it is replaced in each place where \(k\) occurs) \[S_{n}=\sum_{k=1}^{n}f(x_{k}^{*})\Delta_{k}x=\sum_{i=1}^{n}f(x_{i}^{*})\Delta_{i}x.\] Similarly, the letter \(x\) chosen for the variable of integration in \(\int_{a}^{b}f(x)dx\) is a dummy variable, which disappears in the final result. In other words, it can be replaced by any other letter that we wish without affecting the integral; thus \[\int_{a}^{b}f(x)dx=\int_{a}^{b}f(u)du.\] For example, if \[\int_{1}^{2}f(x)dx=32,\] then \[\int_{1}^{2}f(u)du=32.\] Therefore, instead of \(\int_{a}^{b}f(x)dx\), sometimes we may simply write \[\int_{a}^{b}f.\] Unlike the case of the definite integral, the variable of integration in an indefinite integral is not a dummy variable because it appears in the final result. For example, \[\int xdx=\frac{1}{2}x^{2}+C_{1},\quad\int udu=\frac{1}{2}u^{2}+C_{2}\] and in this sense \[\int xdx\neq\int udu.\] In the previous discussion, we assumed \(a<b\). However, if we omit this condition and assume \(b<a\), we can still retain our definition of integral; the only change is that we have to number the subdivision points from the right side, which make the differences \(\Delta_{k}x\) negative. We are thus led to the relation \[\int_{b}^{a}f(x)dx=-\int_{a}^{b}f(x)dx.\] In conformity, we define \[\int_{a}^{a}f(x)dx=0.\] \[\int_{\color{red} a}^{\color{blue} b}f(x)dx=-\int_{\color{blue} b}^{\color{red} a}f(x)dx. \tag{ $a$ and $b$ interchanged} \] and \[\int_{a}^{a}f(x)dx=0. \tag{same upper and lower limits} \] The variable of integration is a dummy variable
Hide the explanation about the dummy variable
$\displaystyle{\int_a^b f(x)dx} = $ area above the $x$-axis $-$ area below the $x$-axis (when $a<b$)
Examples
Now let’s solve some examples.
Let divide the interval \([-1,3]\) into \(n\) subintervals of equal width \(\Delta x=(3-(-1))/n=4/n\). In each subinterval \([x_{k},x_{k+1}]\), let use \(x_{k}^{*}=x_{k}\) as the sample point \[\begin{aligned} x_{0} & =-1\\ x_{1} & =-1+\Delta x=-1+\frac{4}{n}\\ x_{2} & =-1+2\Delta x=-1+2\left(\frac{4}{n}\right)\\ & \vdots\\ x_{k} & =-1+k\Delta x=-1+k\left(\frac{4}{n}\right)\\ & \vdots\\ x_{n} & =-1+n\Delta x=-1+n\left(\frac{4}{n}\right)=-1+4=3.\end{aligned}\] Therefore, \(f(x_{k}^{*})=f(x_{k})=2-x_{k}=2-\left[-1+k\left(\frac{4}{n}\right)\right]=3-\frac{4k}{n}\) and \[\begin{aligned} \sum_{k=1}^{n}f(x_{k}^{*})\Delta_{k}x & =\sum_{k=1}^{n}\left(3-\frac{4k}{n}\right)\frac{4}{n}\\ & =\sum_{k=1}^{n}\left(\frac{12}{n}-\frac{16k}{n^{2}}\right)\\ & =\frac{12}{n}\sum_{k=1}^{n}1-\frac{16}{n^{2}}\sum_{k=1}^{n}k\\ & =\frac{12}{n}(n)-\frac{16}{n^{2}}\frac{n(n+1)}{2}\\ & =12-8\left(1+\frac{1}{n}\right)\end{aligned}\] Notice that in the above summation, \(n\) is a fixed number (say \(n=10\)) and not a function of the summation index \(k\). That is why we could move \(n\) outside the sigma sign. For these calculations, we have also used the formulas \(\sum_{k=1}^{n}1=n\) and \(\sum_{k=1}^{n}k=n(n+1)/2\) that we reviewed in the Section on Sigma Notation.
Because the width of each subinterval is the same \(\max\Delta_{k}x=4/n\to0\) is equivalent to \(n\to\infty\), and we can conclude \[\begin{aligned} \int_{-1}^{3}(2-x)dx & =\lim_{n\to\infty}\sum_{k=1}^{n}f(x_{k}^{*})\Delta x\\ & =\lim_{n\to\infty}\left[12-8\left(1+\frac{1}{n}\right)\right]\\ & =12-8(1+0)=4.\end{aligned}\]
You can easily show that if we use \(x_{k}^{*}=x_{k+1}\) (instead of \(x_{k}^{*}=x_{k}\)) as the sample point in each subinterval \([x_{k},x_{k+1}]\), we will arrive at the same result.
Because the graph of \(y=2-x\) is a straight line, we can easily check our answer. We should subtract the area of the part that lies below the \(x\)-axis from the area of the above that is above the \(x\)-axis (see Figure 9). It follows from the familiar triangle area formula \(A=\text{base}\times\text{height}/2\) that \[\int_{-1}^{3}(2-x)dx=\frac{3\times3}{2}-\frac{1\times1}{2}=4.\]
Let’s divide the interval \([1,3]\) into \(n\) subintervals of equal width \(\Delta_{k}x=\Delta x=\frac{(3-1)}{n}=\frac{2}{n}\): \[\begin{aligned} x_{0} & =1\\ x_{1} & =1+\Delta x=1+\frac{2}{n}\\ x_{2} & =1+2\Delta x=1+2\left(\frac{2}{n}\right)\\ & \vdots\\ x_{k} & =1+k\Delta x=1+k\left(\frac{2}{n}\right)\\ & \vdots\\ x_{n} & =1+n\Delta x=1+n\left(\frac{2}{n}\right)=3.\end{aligned}\] Assume \(f(x_{k}^{*})=f(x_{k})=\left(1+\frac{2k}{n}\right)^{2}=1+\frac{4k}{n}+\frac{4k^{2}}{n^{2}}\). Then \[\begin{aligned} \sum_{k=1}^{n}f(x_{k}^{*})\Delta x & =\sum_{k=1}^{n}\left[\frac{2}{n}+\frac{8k}{n^{2}}+\frac{8k^{2}}{n^{3}}\right]\\ & =\frac{2}{n}\sum_{k=1}^{n}1+\frac{8}{n^{2}}\sum_{k=1}^{n}k+\frac{8}{n^{3}}\sum_{k=1}^{n}k^{2}\\ & =\frac{2}{n}n+\frac{8}{n^{2}}\frac{n(n+1)}{2}+\frac{8}{n^{3}}\frac{n(n+1)(2n+1)}{6}\\ & =2+4\frac{n+1}{n}+\frac{4}{3}\left(\frac{n+1}{n}\right)\left(\frac{2n+1}{n}\right)\\ & =2+4\left(1+\frac{1}{n}\right)+\frac{4}{3}\left(1+\frac{1}{n}\right)\left(2+\frac{1}{n}\right)\end{aligned}\] The width of every subinterval is the same and \(\max\Delta_{k}x\to0\) is equivalent to \(n\to\infty\). As \(n\to\infty\), \(\frac{1}{n}\to0\) and hence \[\begin{aligned} \int_{1}^{3}x^{2}dx & =\lim_{n\to\infty}\sum_{k=1}^{n}f(x_{k}^{*})\Delta x\\ & =\lim_{n\to\infty}\left[2+4\left(1+\frac{1}{n}\right)+\frac{8}{6}\left(1+\frac{1}{n}\right)\left(2+\frac{1}{n}\right)\right]\\ & =2+4(1+0)+\frac{4}{3}(1+0)(2+0)\\ & =\frac{26}{3}.\end{aligned}\]
There are no formulas from elementary geometry that can help us verify our answer (see Figure 10), but we will soon learn a theorem, called the Fundamental Theorem of Calculus, that enables us to evaluate such definite integrals easily.
We know how the graph of $y=|x|$ looks like. To sketch the graph of $y=|x|-2$, we simply shift the graph of $y=|x|$ downward $2$ units. The net area of the region between the graph of $y=|x|-2$ and the $x$-axis over $[-1,3]$ can be easily computed. According to the following figure, we have
\begin{align*}
\int_{-1}^{3}(|x|-2)dx & =-A_{1}-A_{2}-A_{3}+A_{4}\\
& =-1-\frac{1}{2}-2+\frac{1}{2}\\
& =-3.
\end{align*}
We recognize that the curve $y=\sqrt{1-x^{2}}$ is the upper semi-circle of radius 1 centered at the origin (Figure 12). Because we can easily compute the area between the semi-circle and the $x$-axis, taking the limit of Riemann sums is not required.
\begin{align*}
\int_{-1}^{1}\sqrt{1-x^{2}}\ dx & =\text{area between the semi-circle of radius 1 and the $x$-axis}\\
& =\frac{1}{2}(\text{area of a circle of radius 1)}\\
& =\frac{1}{2}\pi(1)^{2}=\frac{\pi}{2}.
\end{align*}
