What we learn here:
Definition of the Absolute Value
It is frequently desirable to measure how large a quantity is, regardless of its sign. In such cases, we use merely the absolute value of the quantity.
The absolute value (or modulus) of a real number $x$, is a nonnegative real number denoted by $|x|$, and defined as follows
\[|x|=\begin{cases}
x & \text{if } x >0 \\
0 & \text{if } x=0\\
-x & \text{if } x<0
\end{cases}\]
- Geometrically the absolute value of a number $x$ is its distance from $0$ regardless of the direction.
- In computer languages and mathematical packages, the absolute value of $x$ is often denoted by abs(x).
Properties of the Absolute Value
- By definition, we have
\[-|x|\leq x\leq|x|\]
because if $x>0$, then $|x|=x$ and we have the sign of equality on the right and the sign of inequality on the left (a positive number is larger than a negative one). If $x<0$, then $|x|=-x$, and we have the sign of equality on the left and the sign of inequality on the right. [Note that $a\leq b$ means $a<b$ or $a=b$]
From the definition of the absolute value, it follows that for every real numbers $a$ and $b$ we have:
- $|a|\geq0$
- $|a|=0$ if and only if $a=0$
- $||a||=|a|$ (the absolute value of the absolute value of $a$ is the absolute value of $a$ because $|a|\ge0$)
- $|-a|=|a|$.
- $|ab|=|a|\ |b|$.
- $\left|\dfrac{a}{b}\right|=\dfrac{|a|}{|b|}$ (provided $b\neq0$)
- If $r>0$
| $|x|\le r$ | is equivalent to | $-r\le x\le r$ | (i) | |
| $|x|\ge r$ | is equivalent to | $-x\le r$ or $r\geq x$ | (ii) | |
| $|x|=r$ | is equivalent to | $x=r$ or $x=-r$ | (iii) |
8. $|a+b|\leq |a|+|b|$ (known as triangle inequality)
\[|a|=|(a+b)-b|\leq|a+b|+|-b|=|a+b|+|b|\]
\[\Rightarrow|a|-|b|\leq|a+b|.\]
Therefore, always we have
\[\boxed{|a|-|b|\leq|a+b|\leq|a|+|b|.}\]
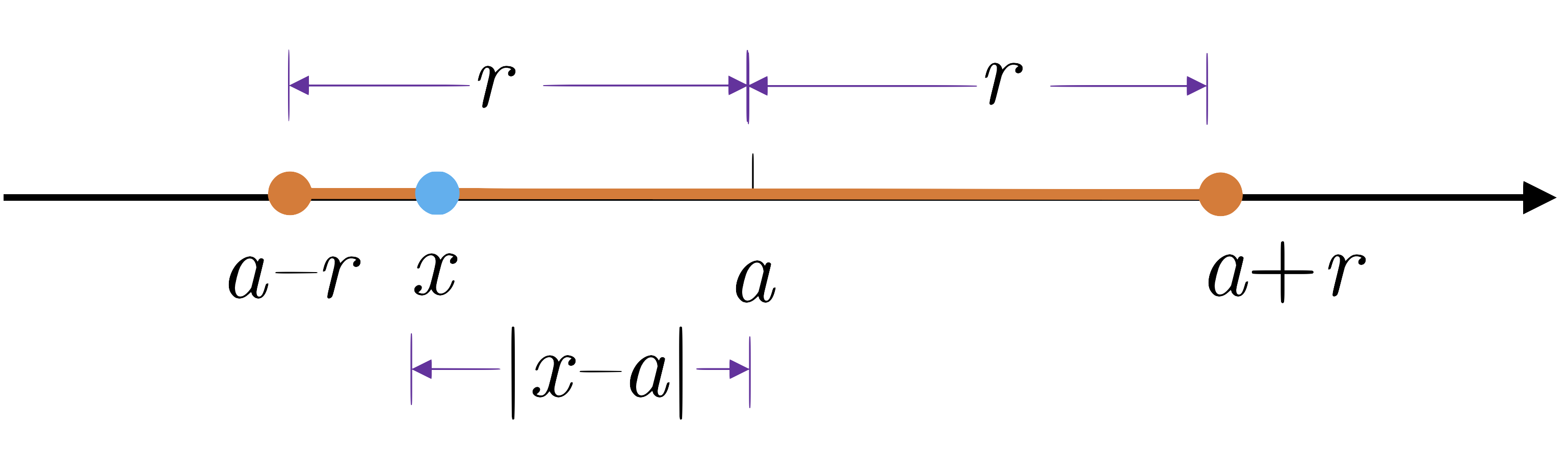
By distance between two numbers, we often mean the value of the larger less the smaller. Thus the distance between 4 and 10 is 6, and the distance between 10 and 4 is also 6 . Let $a$ and $b$ be two real numbers. Then, the distance between the points $a$ and $b$ on the number line, denoted by $d(a,b)$, is \[d(a,b)=|a-b|.\]
It follows from Equation (ii) that for any real number $a$ and any positive number $r$, \[|x-a|<r\]
is equivalent to \[-r<x-a<r\]
or if we add $a$ to each side: \[a-r<x<a+r\]
This means that the distance of $x$ from $a$ is less than $r$ if and only if $x$ is between $a-r$ and $a+r$. Let $I$ be the set of all points whose distance from a fixed point $a$ is less than a number $\delta>0$. Then \begin{align*} [For the second equation, we used the fact that $|t|<\delta$ is equivalent to $-\delta<t<\delta$ and for the third equation, we added $a$ to each side] Such a set is called a neighborhood (or more precisely the $\delta$-neighborhood) of $a$ and $\delta$ is called the radius of the neighborhood. The $\delta$-neighborhood of $a$ is shown in the following figure. Now let’s consider the set of all points such that \[0<|x-a|<\delta\]
or \[J=\{x|\ 0<|x-a|<\delta\}\]
Here we have two inequalities \[0<|x-a|\quad\text{and}\quad|x-a|<\delta\]
Recall that the absolute value is always nonnegative (that is $0\le|t-a|$ for all $t$) , so \[0<|x-a|\]
means \[|x-a|\neq 0\]
or equivalently \[x\neq a\]
[Recall that $|t|=0$ if and only if $t=0$]. Therefore, \begin{align*} That is $J$ is the $\delta$-neighborhood of $a$ with the midpoint $a$ removed. The set $J$ is called the deleted $\boldsymbol{\delta}$–neighborhood or punctured neighborhood of $a$. The deleted $\delta$-neighborhood of $a$ is shown in the following figure. Distance Between Numbers
I & =\{x|\ |x-a|<\delta\}\\
& =\{x|\ -\delta<x-a<\delta\}\\
& =\{x|\ a-\delta<x<a+\delta\}
\end{align*}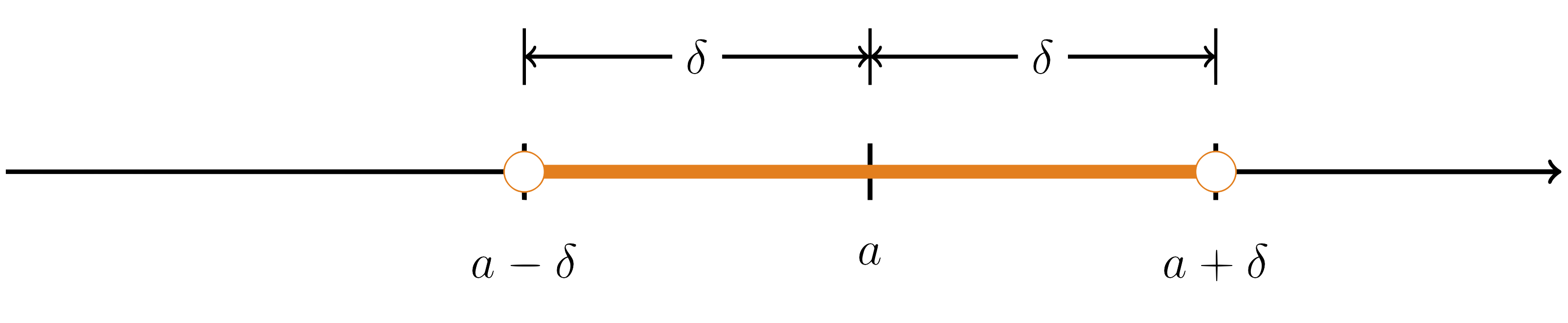
J & =\{x|\quad0<|x-a|<\delta\}\\
& =\{x|\ |x-a|<\delta\quad\text{and}\quad x\neq a\}
\end{align*}

 You can show the significance of the other two statements geometrically.
You can show the significance of the other two statements geometrically.
