1.13 Factorization

To expand algebraic expressions, we need to use the distributive property. The reverse of expansion, called factorization or factoring, consists of using the distributive property in reverse and writing the expression as product of simpler ones. For example, we can write

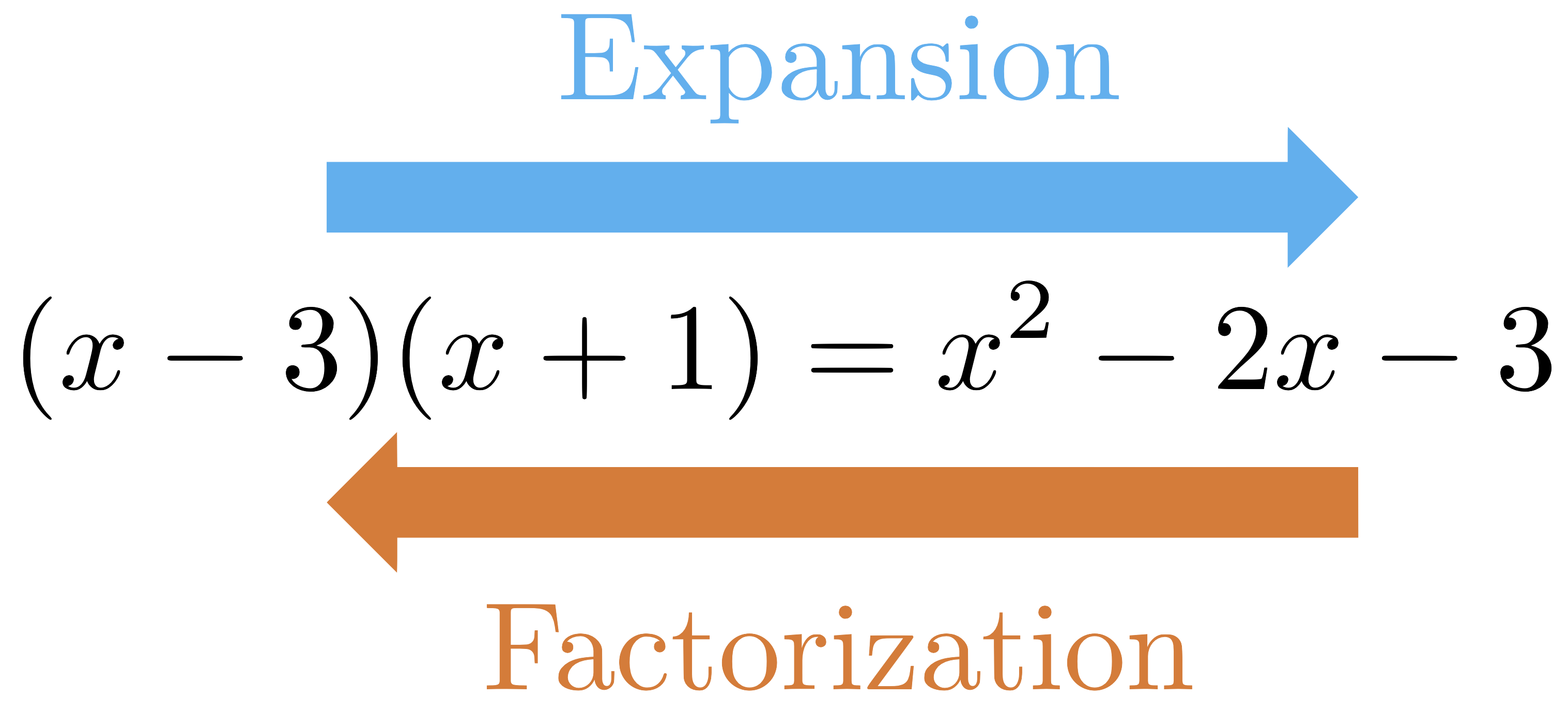
We say that $x-3$ and $x+1$ are factors of $x^{2}-2x-3$.

Click here to read why factorization is important

Factorization has many applications. Here are a number of them.

Solving equations: If we can put an equation in a factored form $P\cdot Q=0$ (where $P$ and $Q$ are two expressions), then solving the problem reduces to solving two independent and often simpler equations $P=0$ and $Q=0$. (Recall if $ab=0$ then $a=0$ or $b=0$). For example instead of solving

\[x^{2}-2x-3=0\]

because $x^{2}-2x-3=(x-3)(x+1)$, we can solve

\[x-3=0\quad\text{or}\quad x+1=0\]

which shows at once

\[x=3\quad\text{or}\quad x=-1.\]

Similarly because

\[x^{3}-8x^{2}+17x-10=(x-1)(x-2)(x-5)\]

we immediately conclude

\[x^{3}-8x^{2}+17x-10=0\Rightarrow x=1\quad\text{or}\quad x=2\quad\text{or}\quad x=5.\]

 Evaluating expressions: It is often easier to evaluate polynomials in the factored form. For example, evaluating $x^{3}-8x^{2}+17x-10$ reduces to only three subtractions and two multiplications if we use its factored form $(x-1)(x-2)(x-5)$.

Determining sign of the output: Sometimes, we need to find out for which values of the variable (often denoted by $x$) a polynomail is positive and for which values it is negative. Doing so is often much easier if we use the factored forms. 

Simplifying rational expressions: Another application of factorization can be simplification of rational expressions. For example, $(x^{2}-1)/(x^{2}-2x-3)$ can be simplified as \[\frac{x^{2}-1}{x^{3}-2x-3}=\frac{(x-1)\cancel{(x+1)}}{(x-3)\cancel{(x+1)}}=\frac{x-1}{x-3}\qquad(x\neq-1)\]

  However, factorization is not always possible and when it is possible, it does not necessarily yield simpler factors. For example, $x^{5}-32$ can be factored into $x-2$ and $x^{4}+2x^{3}+4x^{2}+8x+16$, but obviously we would rather solve $x^{5}-32=x^{5}-2^{5}=0$ than solve the following two equations

\[x-2=0,\quad x^{4}+2x^{3}+4x^{2}+8x+16=0.\]

Now let’s review some techniques of factorization.

Common Factors

When there is a factor common to every term of an expression, we can simply factor it out by applying the distributive property in reverse.

Example 1
Factor each expression

(a) $12x^{3}-15x^{2}$ 

(b) $4x^{5}-8x^{4}-16x^{3}-20x^{2}$

(c) $(2x-5)(3x-7)+4(3x-7)$

Solution

(a) The greatest common factor of the terms $12x^{3}$ and $-15x^{2}$ is $3x^{2}$, so we have

\[12x^{3}-15x^{2}=3x^{2}(4x-5)\]

(b) The greatest common factor of all terms is $4x^{2}$, so we have

\[4x^{5}-8x^{4}-16x^{3}-20x^{2}=4x^{2}\left(x^{3}-2x^{2}-4x-5\right).\]

(c) The greatest common factor of $(2x-5)(3x-7)$ and $4(3x-7)$ is $(3x-7)$. Thus

\begin{align*}
(2x-5)(3x-7)+4(3x-7) & =(3x-7)\left[(2x-5)+4\right]\\
& =(3x-7)(2x-1)
\end{align*}

Factoring Expressions with Fractional Exponents

In calculus sometimes we need to factor expressions with fractional or negative exponents. In this case, we factor out the common factor with the smallest exponent.
 
Example 2

Factor each expression

(a) $x^{3/2}+4x^{1/2}-7x^{-1/2}$

(b) $(x-4)^{-3/5}+5(x-4)^{2/5}$

Solution

(a) The common factor is $x$ and its smallest exponent is $-1/2$. Thus

\[x^{3/2}+4x^{1/2}-7x^{-1/2}=x^{-1/2}(x^{2}+4x-7)\]

Note that $x^{-1/2}x^{2}=x^{(2-1/2)}=x^{3/2}$ and $x^{-1/2}x=x^{(1-1/2)}=x^{1/2}$.

(b) The common factor is $x-4$ and its smallest exponent is $-3/5$. Thus

\begin{align*}
(x-4)^{-3/5}+5(x-4)^{2/5} & =(x-4)^{-3/5}\left[1+(x-4)^{1}\right]\\
& =(x-4)^{-3/2}(x-3).
\end{align*}

Note $(x-4)^{-3/5}\cdot(x-4)=(x-4)^{(1-3/5)}=(x-4)^{2/5}$.

Factorization of polynomials of the form $x^2+bx+c$

Because

\[(x+p)(x+q)=x^{2}+(p+q)x+pq\]

we can factor polynomials of the form $x^{2}+bx+c$ if we can find numbers $p$ and $q$ such that

\[p+q=b\quad\text{and}\quad pq=c.\]

In this section, we choose $p$ and $q$ by trial and error, but technically we can choose them systematically (see the Section on Solutions and Roots).

Example 3

Factor each expression

(a) $x^{2}+3x+2$

(b) $x^{2}-2x-15$

Solution

(a) We need to find $p$ and $q$ such that $p+q=3$ and $pq=2$. By trial and error we find that they are 2 and 1. Thus the factorization is

\[x^{2}+3x+2=(x+2)(x+1).\]

(b) We need to choose $p$ and $q$ such that $p+q=-2$ and $pq=-15$. By trial and error we find that they are $-5$ and $3$. Thus

\[x^{2}-2x-15=(x-5)(x+3).\]

Special Factorization Formulas

If there is no common factor, to factor algebraic expressions we can sometimes use the following formulas that we reviewed in Section 1.12 and reverse the process.

  1.   $A^{2}-B^{2}=(A+B)(A-B)$ (Difference of Squares)
  2.  $A^{2}\pm2AB+B^{2}=(A\pm B)^{2}$ (Perfect Square)
  3.  $A^{3}-B^{3}=(A-B)(A^{2}+AB+B^{2})$ (Difference of Cubes)
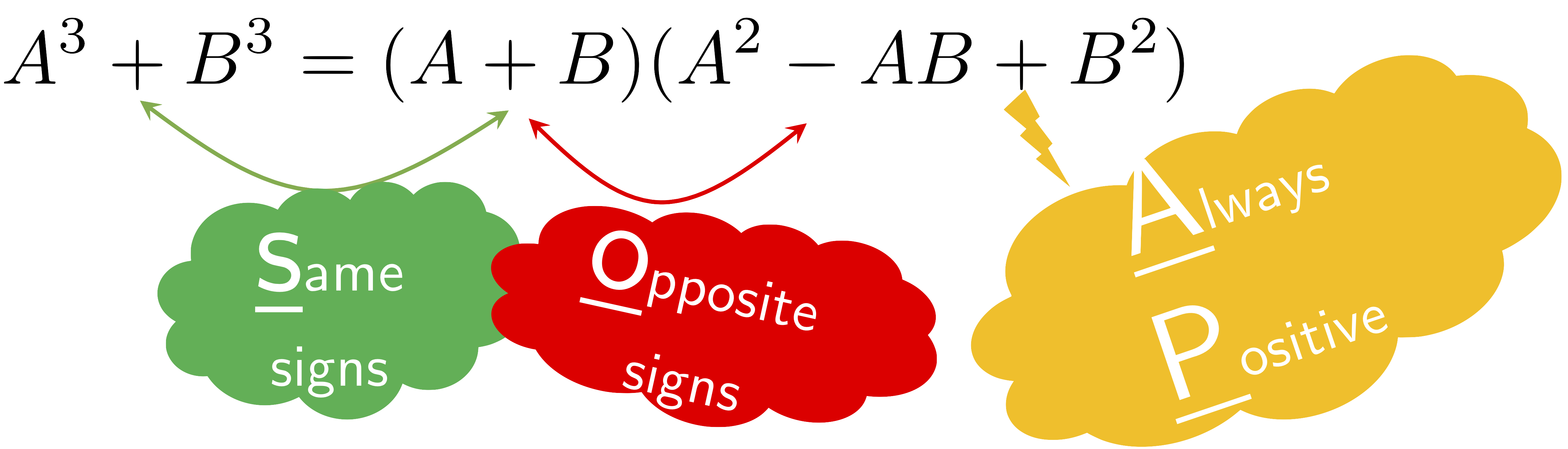
  4.  $A^{3}+B^{3}=(A+B)(A^{2}-AB+B^{2})$  (Sum of Cubes)
 

Mnemonics for Memorizing the Sum/Difference of Cubes Formulas: 

Remember a cube of SOAP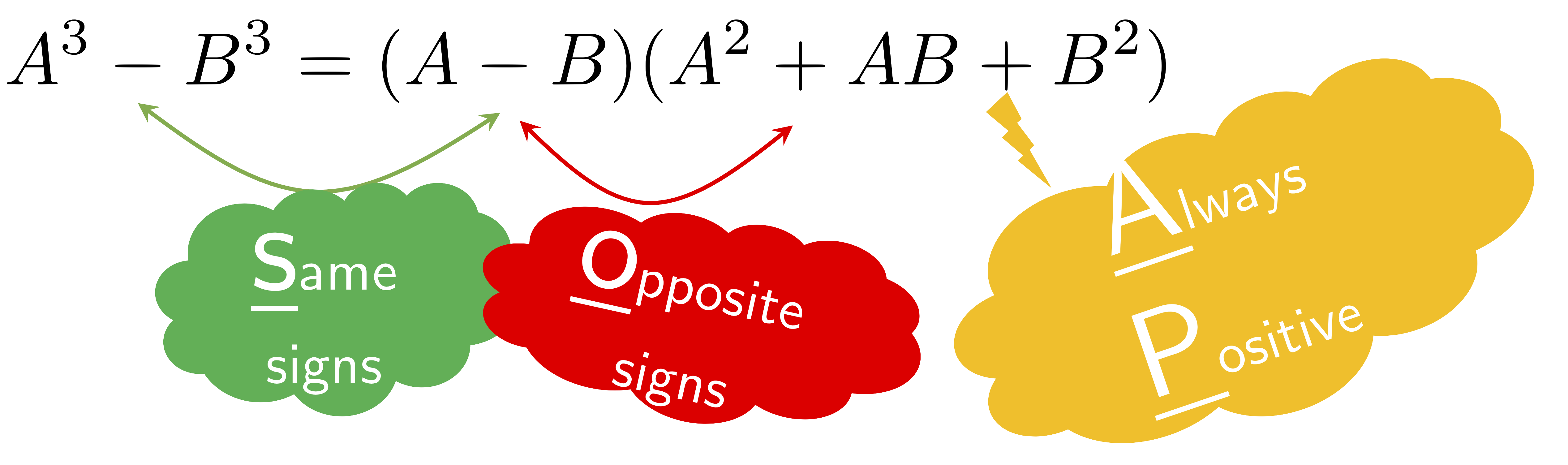

 

Example 4
  Factor each expression 

(a) $9x^{2}-49$

(b) $x^{4}-16$

(c) $x^{2}+10x+25$

(d) $x^{3}-27$

(e) $8x^{3}+64$

Solution
 (a) Rewriting as difference of squares

\[9x^{2}-49=(3x)^{2}-7^{2}\]

Let $A=3x$ and $B=7$ in $A^{2}-B^{2}=(A-B)(A+B)$. Then

\begin{align*}
(3x)^{2}-7^{2} & =A^{2}-B^{2}\\
& =(A-B)(A+B)\\
& =(3x-7)(3x+7).
\end{align*}

(b) Let $A=x^{2}$ and $B=4$, then

\begin{align*}
x^{4}-16 & =A^{2}-B^{2}\\
& =(A-B)(A+B)\\
& =(x^{2}-4)(x^{2}+4)
\end{align*}

We note that we can rewrite $x^{2}-4$ as $x^{2}-2^{4}$, so we can use the Difference of Squares formula and factor it as

\[x^{2}-2^{2}=(x-2)(x+2)\]

Thus

\begin{align*}
x^{4}-16 & =(x^{2}-4)(x^{2}+4)\\
& =(x-2)(x+2)(x^{2}+4).
\end{align*}

(c) Let $A=x$ and $B=5$. Because the middle term $10x=2AB$, the polynomial is a perfect square. By the Perfect Square formula we have

\[x^{2}+10x+25=(x+5)^{2}.\]

(d) Let $A=x$ and $B=3$, then

\begin{align*}
x^{3}-27 & =A^{3}-B^{3}\\
& =(A-B)(A^{2}+AB+B^{2})\\
& =(x-3)(x^{2}+3x+9).
\end{align*}

(e) Here the terms $8x^{3}$ and 64 have the common factor 8, so first of all we factor it out.

\[8x^{3}+64=8(x^{3}+8).\]

Then we can use the Sum of Cubes formula with $A=x$ and $B=2$:

\begin{align*}
x^{3}+8 & =A^{3}+B^{3}\\
& =(A+B)(A^{2}-AB+B^{2})\\
& =(x+2)(x^{2}-2x+4).
\end{align*}

Therefore

\begin{align*}
8x^{3}+64 & =8(x^{3}+8)\\
& =8(x+2)(x^{2}-2x+4).
\end{align*}

Click here for more special factorization formulas

In general we can factor the sum or difference of two $n$th power ($n$ an integer) as follows

Difference, even exponent:

$A^{2n}-B^{2n}=(A^{n}-B^{n})(A^{n}+B^{n})$

Difference, even or odd exponent:

$A^{n}-B^{n}=(A-B)(A^{n-1}+A^{n-2}B+A^{n-3}B^{2}+\cdots+AB^{n-2}+B^{n-1})$

If we replace $B$ with $-B$ in the above formula and $n$ is odd then we will get the following formula (Note that if $n$ is even, we won’t get a new formula).

Sum, odd exponent:

$A^{n}+B^{n}=(A+B)(A^{n-1}-A^{n-2}B+A^{n-3}B^{2}-\cdots-AB^{n-2}+B^{n-1})$

Sum, even exponent:

$A^{n}+B^{n}$ cannot, in general, be factored.

 

 

 Factorization by Grouping Terms

Sometimes there is no a common factor (other than $\pm1$) to all terms of a polynomial. However, the polynomial can sometimes be factored if we suitably group the terms that have common factors. This strategy may work for polynomials with at least four terms.

For example, we can factor the polynomial $x^{3}+3x^{2}+4x+12$ if we group the first two terms together and the last two terms together and then factor each group, namely

\begin{align*}
x^{3}+3x^{2}+4x+12 & =(x^{3}+3x^{2})+(4x+12)\\
& =x^{2}(x+3)+4(x+3)\\
& =(x+3)(x^{2}+4)
\end{align*}

For the last equation, we have factored out the common factor $x+3$.

Example 5

Factor $2x^{3}+x^{2}-18x-9$.

Solution

\begin{align*}
2x^{3}+x^{2}-18x-9 & =(2x^{3}+x^{2})-(18x+9) &  {\small \text{ (Group terms)}}\\
& =x^{2}(2x+1)-9(2x+1) &  {\small \text{ (Factor out common factor of each group)}}\\
& =(2x+1)(x^{2}-9) & {\small \text{ (Factor out } (2x+1))}\\
& =(2x+1)(x-3)(x+3) & {\small \text{ (Use Difference of Squares formula)}}
\end{align*}