In this section, we introduce the concept of intervals that are extensively used in calculus. The set of all real numbers that lie between two given numbers and may or may not include these end points is called an interval.
- Closed interval $[ a,b ]$ is the set of real numbers $x$ that satisfy the inequalities $a \leq x \leq b$. \[ [a,b]=\{x\in\mathbb{{R}}|\ a\leq x\leq b\}.\]
- Open interval $( a,b )$ is the set of real numbers $x$ that satisfy the inequalities $a<x<b$. \[ (a,b)=\{x\in\mathbb{{R}}|\ a<x<b\}.\]
Another notation for the open interval $( a,b )$ is $]a,b[$.
We also have half-open intervals that include only one endpoint. In addition to finite intervals, we have infinite intervals that extend indefinitely in one or both directions. If an interval extends indefinitely in the positive direction, we write $\infty$ (or sometimes $+\infty$) in place of the right end and if it extends indefinitely in the negative direction, we write $-\infty$ in place of the left end. All of these cases are shown in the following table.
- We always denote the inclusion of an end in an interval by square bracket and its exclusion by a parenthesis.
-
The symbols $\infty$ and $-\infty$ (read “infinity” and “minus infinity”) are not real numbers. We use these symbols to indicate that the interval extends indefinitely in a direction, so “a real number cannot be equal to infinity. That’s why when one end of an interval is $\infty$ or $-\infty$, that end is denoted by a parenthesis.
| Notation | Definition | Graph | Classification |
| $[a,b]$ |
$\{x|\ a\leq x\leq b\}$
|
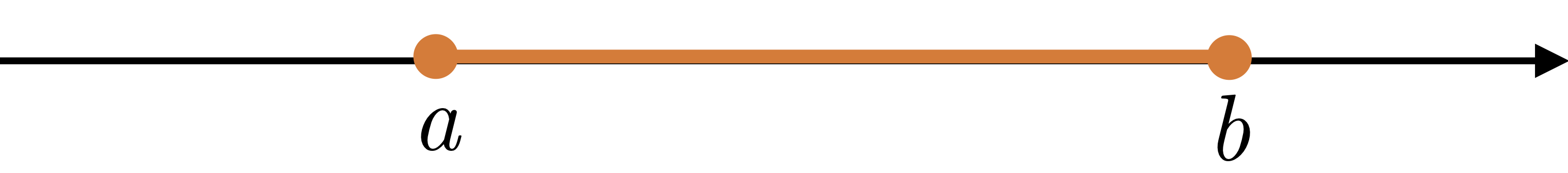 |
finite, closed |
| $(a,b)$ | $\{x|\ a< x< b\}$ | 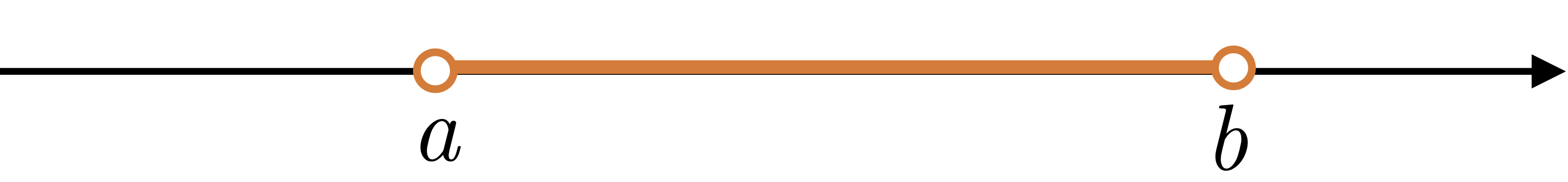 |
finite, open |
| $[a,b)$ | $\{x|\ a\leq x< b\}$ | 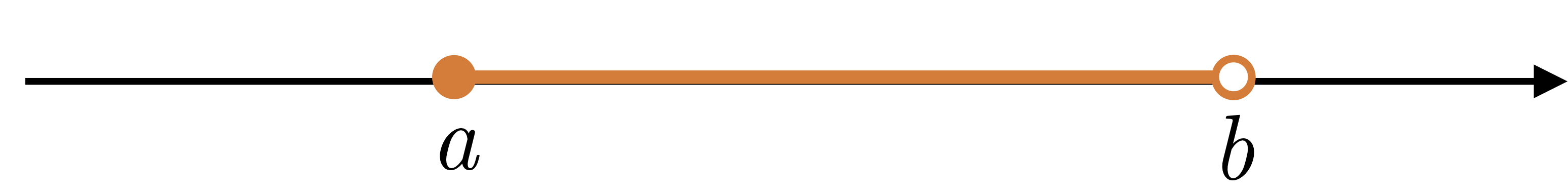 |
finite, half-open |
| $(a,b]$ | $\{x|\ a< x\leq b\}$ | 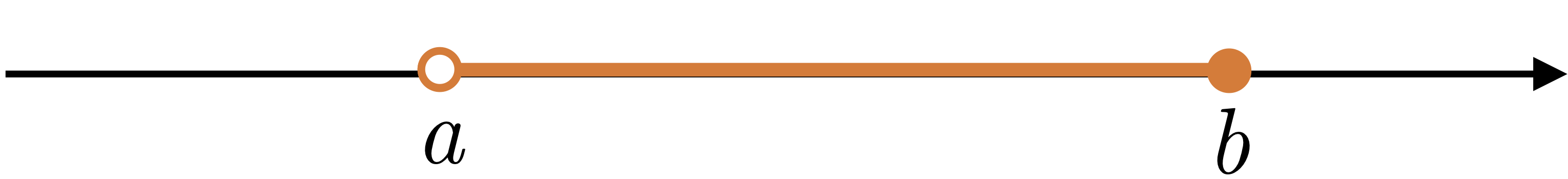 |
finite, half-open |
| $[a,\infty)$ | $\{x|\ a\leq x< \infty\}$ | 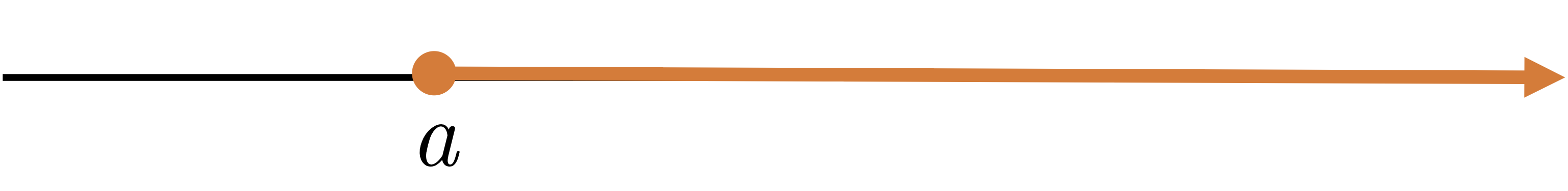 |
infinite, closed |
| $(a,\infty)$ | $\{x|\ a< x< \infty\}$ |  |
infinite, open |
| $(-\infty,b]$ | $\{x|\ -\infty< x\leq b\}$ | 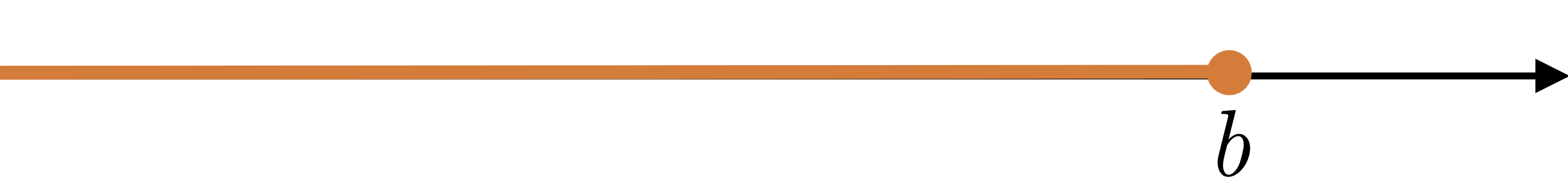 |
infinite, closed |
| $(-\infty,b)$ | $\{x|\ -\infty< x< b\}$ | 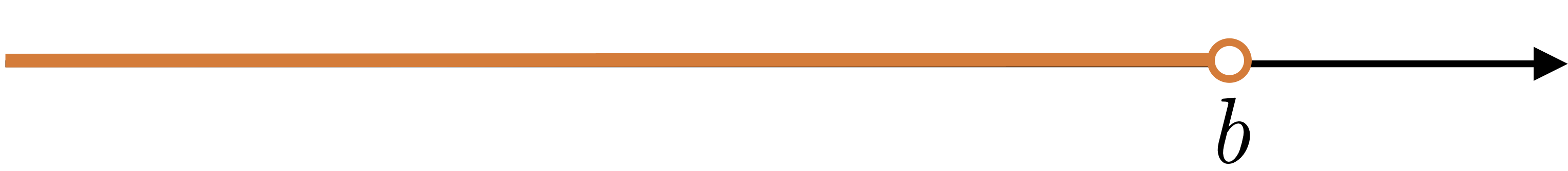 |
infinite, open |
| $(-\infty,\infty)$ | $\{x|\ -\infty< x< \infty\}$ |  |
infinite, open, closed |
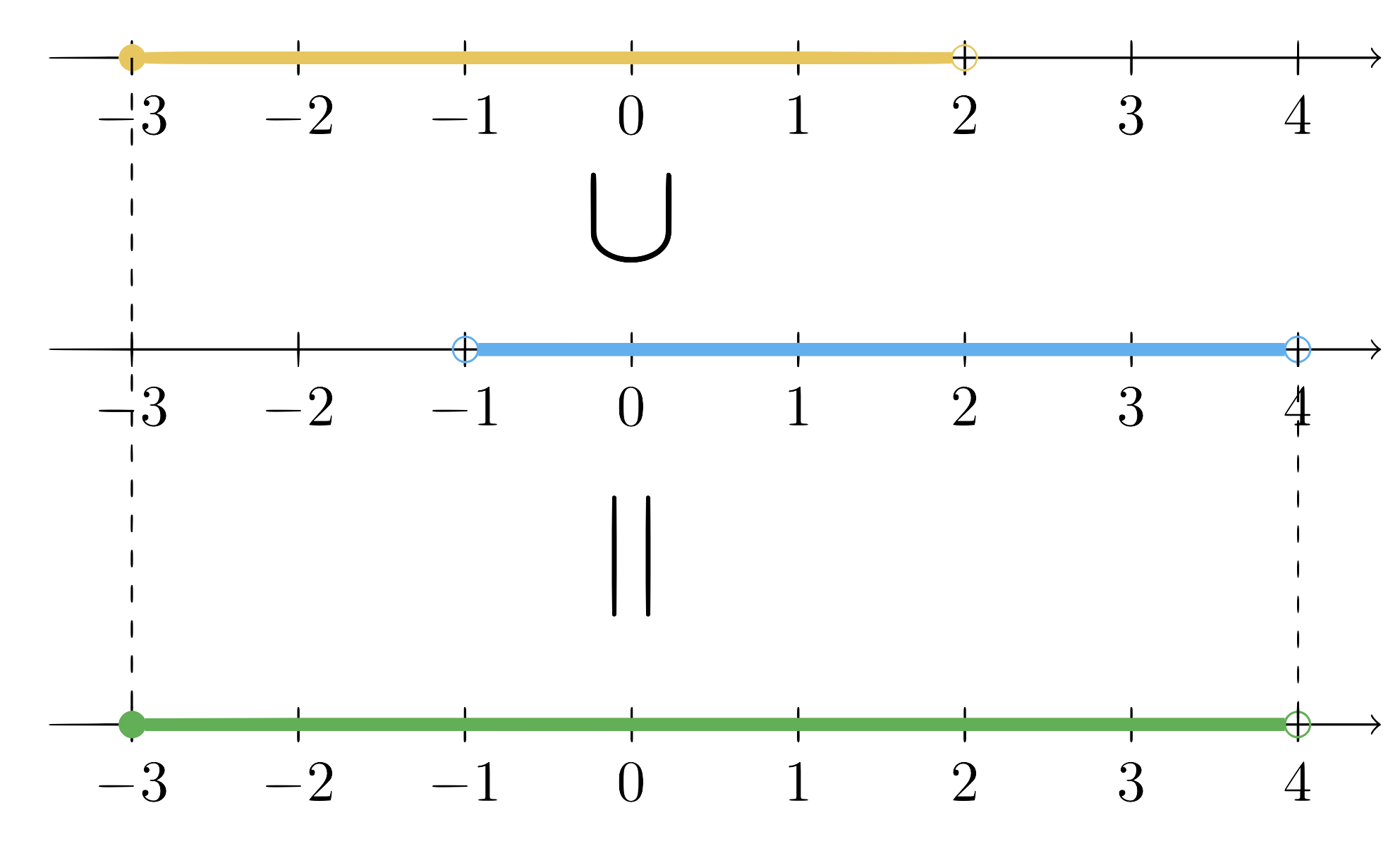
- Because intervals are sets, we can calculate the union, intersection, and difference of intervals (For more information about set operations see this page). For example the set \[\{x|\ x\neq3\}\] can be written as \[(-\infty,3)\cup(3,\infty)\] or \[\mathbb{R}-\{3\}\] The following figure shows this set.

- To avoid any mistakes in set calculations on intervals, you can picture them graphically.