3.9 Linear or Affine Approximation

In single variable calculus, we learned that the tangent line to the graph of $y = f (x)$ at $x = x_{0}$ gives a good approximation of $f (x)$ near $x_{0}$ if $f^{'} (x_{0})$ exists: $f (x) \approx L (x) = f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) .$ Here $L (x)$ is called the linearization [1] of $f$ at the point $x$ (see Fig. 1).

Figure 1 : Linearization in 2D-The tangent plane at

(x_{0}, y_{0}, f (x_{0}, y_{0}))

is close to the graph of

f

for points

(x, y)

close to

(x_{0}, y_{0})

Similarly, for 2D problems, the tangent plane to the graph of $z = f (x, y)$ at the point $P = (x_{0}, y_{0}, z_{0})$ gives a good approximation to the function near $(x_{0}, y_{0})$ if the function is “smooth enough” (see Fig. 2):

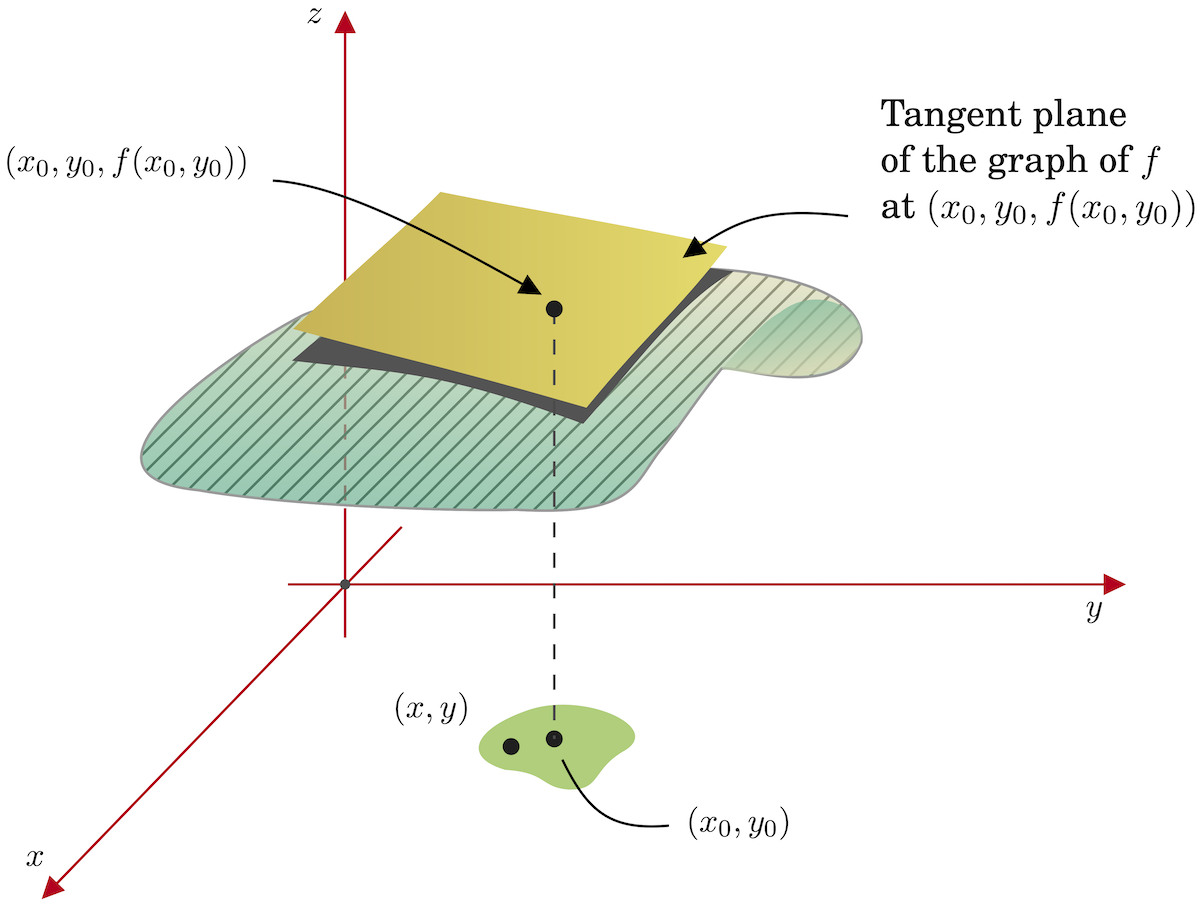
Figure 2: The tangent plane at $(x_{0}, y_{0}, f (x_{0}, y_{0}))$ is close to the graph of $f$ for points $(x, y)$ close to $(x_{0}, y_{0})$

Definition 1. If $z = f (x, y)$ , the function $L (x, y)$ which is given by the following equation is called the linearization of $f$ at $(x_{0}, y_{0})$ $L (x, y) = f (x_{0}, y_{0}) + f_{x} (x_{0}, y_{0}) (x - x_{0}) + f_{y} (x_{0}, y_{0}) (y - y_{0}) .$ If $f$ is “smooth enough”, then for $(x, y)$ near $(x_{0}, y_{0}) :$ $f (x, y) \approx L (x, y)$

Example 1

Find the value of $f (0.2, - 0.1)$ approximately if $f (x, y) = \cos x e^{2 y}$ .

Solution

We can use linear approximation of $f$ at $(0, 0)$ , where $f$ and its partial derivatives can be easily evaluated: $f (0, 0) = 1$ $\begin{aligned} f_{x} (x, y) = - \sin x e^{2 y} \Rightarrow & f_{x} (0, 0) = 0 \\ f_{y} (x, y) = 2 \cos x e^{2 y} \Rightarrow & f_{y} (0, 0) = 2 \end{aligned}$ Therefore $L (x, y) = 1 + 0 \times (x - 0) + 2 \times (y - 0)$ , which approximates $f (0.2, - 0.1)$ $f (0.2, - 0.1) \approx L (0, 2, - 0.1) = 1 + 2 \times (- 0.1) = 0.8$

The exact value of $f (0.2, - 0.1) = 0.8024$ , which means the error in this approximation is $\approx 0.3 %$

Extension to Functions of More Than Two Variables

We can easily extend the concept of the linearization of functions of more than two variables. For example, if $u = f (x, y, z)$ , then its linearization at $(x_{0}, y_{0}, z_{0})$ is given by:
$L (x, y, z) = f (x_{0}, y_{0}, z_{0}) + f_{x} (x_{0}, y_{0}, z_{0}) \cdot (x - x_{0}) + f_{y} (x_{0}, y_{0}, z_{0}) \cdot (y - y_{0}) + f_{z} (x_{0}, y_{0}, z_{0}) \cdot (z - z_{0})$
or $L (x, y, z) = f (x_{0}, y_{0}, z_{0}) + \frac{\partial f}{\partial x} (x_{0}, y_{0}, z_{0}) \cdot (x - x_{0}) + \frac{\partial f}{\partial y} (x_{0}, y_{0}, z_{0}) \cdot (y - y_{0}) + \frac{\partial f}{\partial z} (x_{0}, y_{0}, z_{0}) \cdot (z - z_{0})$

If $u = f (x_{1}, \dots, x_{n})$ , its linearization at the point $p = (a_{1}, \dots, a_{n})$ is $L (x_{1}, \dots, x_{n}) = f (p) + {\frac{\partial f}{\partial x_{1}} |}_{p} (x - a_{1}) + \dots + {\frac{\partial f}{\partial x_{n}} |}_{p} (x - a_{n})$

In the following example, we want to know whether we can approximate a function with its linearization if it is not smooth enough?

Example 2

Given $f (x, y) = {\begin{cases} \frac{x y}{x^{2} + y^{2}} & if (x, y) \neq (0, 0) \\ 0 & if (x, y) = (0, 0) \end{cases},$ using the linearization of $f$ at $(0, 0)$ , approximate $f (0.01, - 0.01)$ and compare it with its exact value.

Graph of

f (x, y) = \frac{x y}{x^{2} + y^{2}}

Solution

To calculate $f_{x} (0, 0)$ and $f_{y} (0, 0)$ , we have to use the definition of partial derivatives: $f_{x} (0, 0) = lim_{h \to 0} \frac{f (0 + h, 0) - f (0, 0)}{h} = lim_{h \to 0} \frac{\frac{h \times 0}{h^{2} + 0^{2}} - 0}{h} = lim_{h \to 0} \frac{0 - 0}{h} = 0,$ $f_{y} (0, 0) = lim_{k \to 0} \frac{f (0, 0 + k) - f (0, 0)}{k} = lim_{k \to 0} \frac{\frac{0 \times k}{0^{2} + k^{2}} - 0}{h} = lim_{k \to 0} \frac{0 - 0}{k} = 0,$ Therefore the linearization of $f$ at $(0, 0)$ reads: $L (x, y) = \underset{= 0}{\underset{⏟}{f (0, 0)}} + \underset{= 0}{\underset{⏟}{f_{x} (0, 0)}} x + \underset{= 0}{\underset{⏟}{f_{y} (0, 0)}} y = 0,$ Therefore $L (0.01, - 0.01) = 0$ . However the exact value of $f (0.01, - 0.01)$ is $- 1 / 2$ .

In this example, $f (x, y) = 0$ on the $x$ and $y$ -axes, $f (x, y) = \frac{1}{2}$ on $x = y$ and $f (x, y) = - \frac{1}{2}$ on $x = - y$ .

This example shows even if $f_{x} (x_{0}, y_{0})$ and $f_{y} (x_{0}, y_{0})$ exist, the linearization does not need to be a good approximation for $f$ near $(x_{0}, y_{0})$ .

[1] Here, we use “linearization” or “linear approximation” loosely. Note that $L (x)$ is not a linear function unless $f (x_{0}) = 0$ , because any linear function has to pass through the origin. More precisely we should say $L (x)$ is an “affine function” and the approximation is the “affine approximation”. An affine function is a function composed of a linear function + a constant.