3.4 Open and Closed Sets

In the calculus of a single variable, we deal with open and closed intervals. The extension of these concepts to two and higher dimensional spaces are open and closed sets. First, we extend the concept of a neighborhood to $\mathbb{R}^n$, which will be later used for the definition of open and closed sets.

Definition 1. Let $\mathbf{x}_0$ be a given point in $\mathbb{R}^n$, and let $r$ be a number $>0$. The set of all points $\mathbf{x}$ in $\mathbb{R}^n$ such that
\[\left|\mathbf{x}-\mathbf{x}_0\right|<r\] is called a neighborhood of $\mathbf{x}_0$ with radius $r$ and is denoted by the symbol $N_r(\mathbf{x}_0)$.
\[N_r(\mathbf{x}_0)=\{\mathbf{x}\in\mathbb{R}^n|\ \left|\mathbf{x}-\mathbf{x}_0\right|<r\}\]

In other words, $N_r(\mathbf{x}_0)$ consists of all points whose distance from the point $\mathbf{x}_0$ is less than $r$.
$N_r(\mathbf{x}_0)$ is also called the open ball of radius $r$ and center $\mathbf{x}_0$.
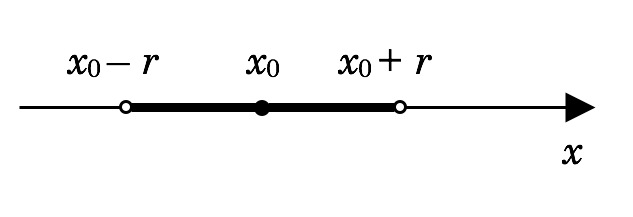
When $n=1$, $N_r(x_0)$ is an open interval with its center at the point $x_0$; that is, $N_r(x_0)=(x_0-r,x_0+r)$ (See Figure 1 (a)).
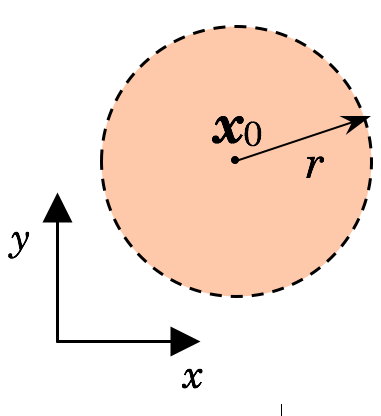
In the plane (or when $n=2$), $N_r(\mathbf{x}_0)$ is a circular disk with center $\mathbf{x}_0=(x_0,y_0)$ and radius $r$ given by the inequality
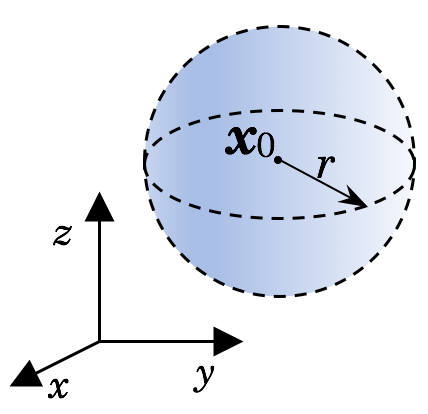
\[\sqrt{(x-x_0)^2+(y-y_0)^2}<r.\] (See Figure 1 (b)).
In $\mathbb{R}^3$, $N_r(\mathbf{x}_0)$ is a spherical solid with center $\mathbf{x}_0=(x_0,y_0,z_0)$ and radius $r$ given by the inequality
\[\sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2}<r.\] (See Figure 1 (c)).
The points $\mathbf{x}$ whose distance from $\mathbf{x}_0$ is exactly $r$ form the boundary of $N_r(\mathbf{x}_0)$.


(a) Open interval	(b) Circular disk	(c) Spherical solid

Figure 1: Neighborhoods in (a) $\mathbb{R}$, (b) $\mathbb{R}^2$, and (c) $\mathbb{R}^3$. Boundary points are not included.

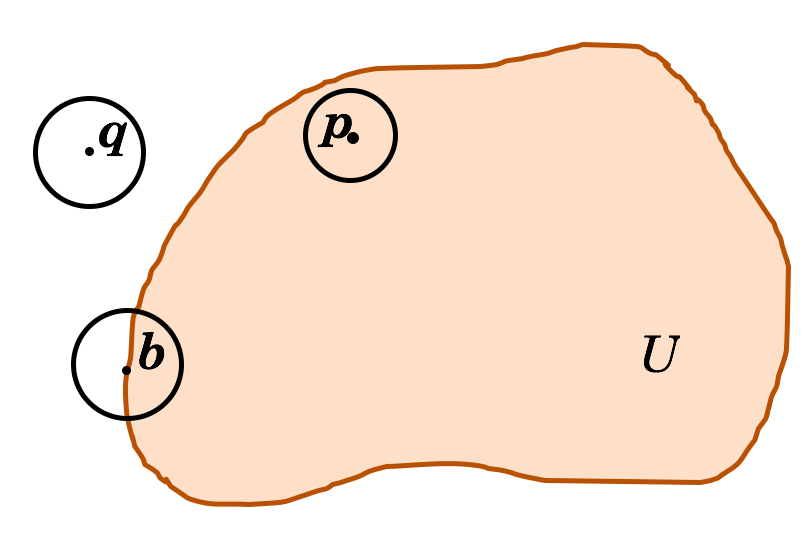
Definition 2. Let $U$ be a set of points in $\mathbb{R}^n$.

A point $\mathbf{p}\in U$ is called an interior point of $U$ if there exists some neighborhood of $\mathbf{p}$ such that all of its points belong to $U$. In other words, there exists $r>0$ such that $N_r(\mathbf{p})\subseteq U$. The set of all interior points of $U$ is called the interior of $U$ and denoted by ${\rm int}(U)$.
A point $\mathbf{b}$ is called a boundary point of $U$, if every neighborhood of $\mathbf{b}$ contains at least one point in $U$ and at least one point not in $U$. The set of all boundary points of $U$ is called the boundary of $U$ and denoted by $\partial U$.
A point $\mathbf{q}$ is called an exterior point of $U$ if it is neither an interior nor a boundary point of $U$. The point $\mathbf{q}$ is an interior point of the complement of $U$, $\mathbb{R}^n-U$. The set of all exterior points of $U$ is called the exterior of $U$ and is denoted by ext$(U)$.

Interior, boundary, and exterior points are depicted in Figure 2. Note that ‘not belonging to $U$’ and ‘exterior to $U$’ are different. A boundary point of $U$ is never an exterior point of $U$, even when it does not belong to $U$.

Figure 2: The point $\mathbf{p}$ is an interior point of the set $ U$, the point $ {\mathbf b}$ is a boundary point of $ U$ and the point $ \mathbf{q}$ is an exterior point of $ U$

Definition 3. A set $U\subseteq \mathbb{R}^n$ is called open if all its points are interior points. In other words, $U$ is open if and only if int $U=U$.

A set $U\subseteq \mathbb{R}^n$ is called closed if its complement $\mathbb{R}^n-U$ is open.

A set is open if and only if it contains no boundary point
A set is closed if and only if it contains its boundary.

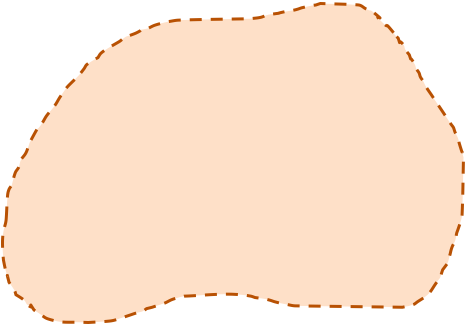
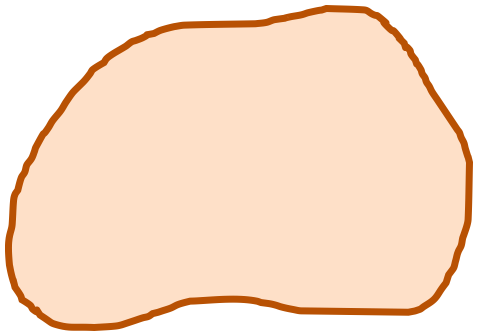
Figure 3 (a) shows an open set because it does not include its boundary. Figure 3 (b) shows a closed set because the set contains its boundary. Figure 3 (c) shows a set that is neither open nor closed, because the set contains some boundary points (so it cannot be an open set) and does not include the entire of its boundary (so it cannot be a closed set).


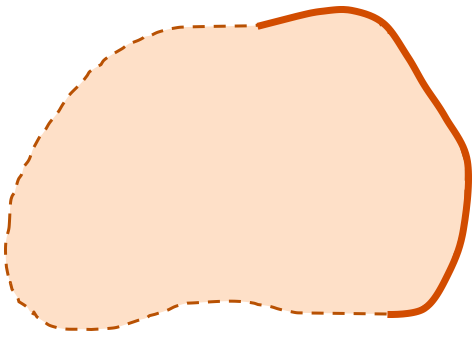(a) Open set	(b) Closed set	(c) neither open nor closed

Figure 3

An open interval $(a,b)$ is an open set in $\mathbb{R}$ because it does not contain its boundary points $x=a$ and $x=b$. A closed interval $[a,b]$ is closed in $\mathbb{R}$, but the intervals $(a,b]$ and $[a,b)$ are neither open nor closed.

The interval $(a,\infty)$ is an open set but the interval $[a,+\infty)$ is a closed set in $\mathbb{R}$.

$\mathbb{R}=(-\infty,\infty)$ is an open set. Therefore, its complement (the empty set) is closed.

The empty set is also an open set (since the empty set has no point, there is no point that is NOT interior. Hence the empty set is an open set); therefore, $\mathbb{R}=(-\infty,\infty)$ is a closed set. In other words, $\mathbb{R}$ and $\emptyset$ are both open and closed.

The union or the intersection of two or more open intervals is open, and the union or the intersection of two or more closed intervals is closed.

The Cartesian product of two open intervals $$(a,b)\times(c,d)=\{(x,y)| a<x<b,\ \text{and}\ c<y<d\}$$ is an open set. The Cartesian product of two closed intervals $$[a,b]\times[c,d]=\{(x,y)| a\leq x \leq b,\ \text{and}\ c\leq y\leq d\}$$ is a closed set. However, $(a,b)\times[c,d]$, $(a,b]\times[c,d], \cdots$ are neither open nor closed.

Note that an open interval in $\mathbb{R}$ is not an open set when it is considered as a subset of $\mathbb{R}^2$, because any neighborhood of its points contains some points that do not belong to this interval. In fact, no subset of $\mathbb{R}$ (except the empty set) is open in $\mathbb{R}^n$.

Let $\mathbf{x}_0\in\mathbb{R}^n$ and $r>0$, then $N_r(\mathbf{x}_0)$ is an open set; due to the strict inequality in Definition 1, $N_r(\mathbf{x}_0)$ does not include any boundary point.