Let \(y=f(x)\) be a continuous function. Suppose \(f\) takes the same value at \(x=a\) and \(x=b\); that is, \(f(a)=f(b)\). Also suppose that \(f'(x)\) exists everywhere between \(a\) and \(b\). The graph of \(f\) is then a continuous curve such that we can draw a tangent line at each point of this curve (see Fig. 1). Geometric intuition shows us at once that for at least one value of \(x\) between \(a\) and \(b\), the tangent is parallel to the \(x\)-axis (say at \(P\)); that is, the slope is zero. This illustrates Rolle’s theorem:
Theorem 1. Rolle’s Theorem. Let \(f(x)\) be a function with the following properties:
- \(f\) is continuous everywhere on the closed interval \([a,b]\),
- \(f'(x)\) exists at each point of the open interval \((a,b)\).
If \(f(a)=f(b)\), then there is at least one point \(c\) in the open interval \((a,b)\) such that \(f'(c)=0\).
This theorem is obviously true, because as \(x\) increases from \(a\) to \(b\), \(f(x)\) cannot always increase or always decrease, since \(f(a)=f(b)\). Hence, for at least one value of \(x\) between \(a\) and \(b\), \(f(x)\) must cease to increase and begin to decrease, or else cease to decrease and begin to increase, and for that particular value of \(x\), the first derivative must be zero (because that particular value of \(x\) is either a local maximum or local minimum point, and Fermat’s Theorem tells us that the first derivative at a local maximum or minimum point must be zero).
- If the conditions of Rolle’s theorem are satisfied, then there is at least one point \(c\in(a,b)\) such that \(f'(c)=0\), but there may be more than one such point in the interval. For example, there are three points for which the derivative of the function is zero in Figure 2.
In a special case where \(f(a)=f(b)=0\), Rolle’s theorem states that between any pairs of roots of \(f(x)\) lies a root of \(f'(x)\).
- We say \(x=a\) is a root of \(f(x)\) if \(f\) vanishes for \(x=a\); that is, \(f(a)=0\). If we plot the graph of \(f\), then this graph crosses the \(x\)-axis at \(x=a\).
For example, let \[f(x)=(x-3)(x-2)(x+1)(x+2)(x+4).\] This function becomes zero at \(x=3,2,-1,-2\), and \(-4\). \(f\) is a polynomial and thus it is continuous and differentiable everywhere. It follows from Rolle’s Theorem that \(f'(x)\) has (at least) one zero in the interval \((2,3)\), one zero in \((-1,2)\), one zero in \((-2,-1)\), and one in \((-2,-4)\) (see Figure 3).
The zeros of \(g(x)=x^{4}-x^{2}-2\) are \(\pm\sqrt{2}\). So Rolle’s Theorem tells us its derivative \(g'(x)=4x^{3}-2x\) has at least one zero between \(-\sqrt{2}\) and \(\sqrt{2}\). In fact, \(g'(x)=2x(2x^{2}-1)\) has three roots between \(-\sqrt{2}\) and \(\sqrt{2}\). The roots are \(x=0\) and \(x=\pm1/\sqrt{2}\) (see Figure 4).
Let \[f(x)=x^{3}+x-1.\] Because \(f\) is a polynomial, it is continuous everywhere. Because \[f(-1)=(-1)^{3}+(-1)-1=-3<0\] and \[f(1)=1^{3}+1-1=1>0,\] it follows from Bolzano’s Theorem (or more generally the Intermediate-Value Theorem), that \(f\) has at least one zero between \(-1\) and \(1\). If \(f\) had more than one zero, Rolle’s Theorem would guarantee the existence of a zero (a root) of \(f'(x)\). However, the derivative of \(f\) is always positive: \[f'(x)=3x^{2}+1>0.\] This means that \(f\) cannot have more than one root.
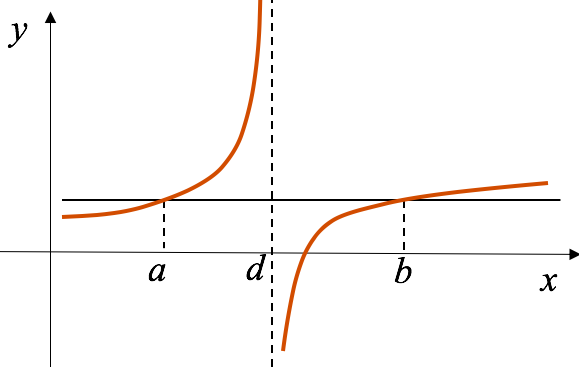
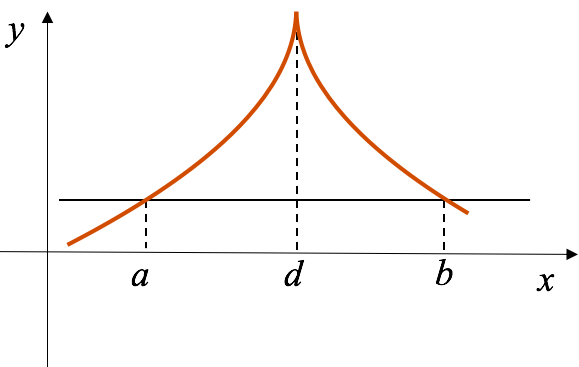
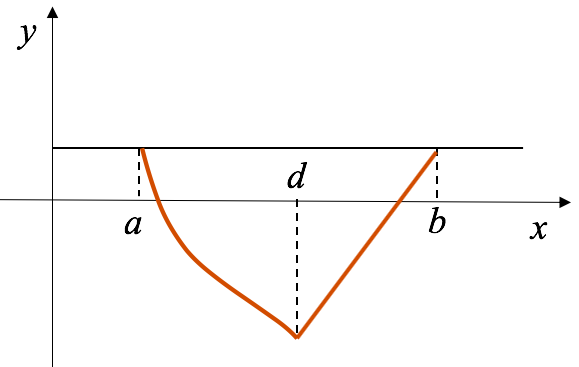
We need to emphasize that \(f(x)\) must be continuous at all points in the closed interval \([a,b]\), including the endpoints, but its derivative does not need to exist at the endpoints. If \(f(x)\) is discontinuous even at one point of the closed interval or \(f'(x)\) does not exist at an interior point of the interval, then Rolle’s rule does not apply. For example, Fig. 6(a) shows the graph of a function that is discontinuous (goes to \(\pm\infty\)) for \(x=d\), a value lying between \(a\) and \(b\). Figure 6(b) and (c) show the graph of continuous functions whose first derivatives are discontinuous for such an intermediate value \(x=d\). In all of these cases, it is seen that at no point on the graph between \(x=a\) and \(x=b\) does the tangent to the curve become parallel to the
\(x\)-axis.
 |
 |
 |
| (a) | (b) | (c) |
| Figure 6 | ||
This function is continuous in \([-2,2]\) and we know \(f(2)=f(-2)=2\). The derivative of this function \(f'(x)\) is 1 for \(0<x\leq2\), \(-1\) for \(-2\leq x<0\), and does not exist for \(x=0\).
\[f'(x)=\begin{cases} 1 & \text{if }0<x<2\\ \text{does not exist} & \text{if }x=0\\ -1 & \text{if }-2< x<0 \end{cases}\]
In other words, \(f'(x)\) nowhere vanishes; this function does not follow Rolle’s theorem. The failure can be explained by the fact that \(f'(x)\) does not exist for \(x=0\) which is an interior point of the interval.
The function \(f(x)=\sqrt{1-x^{2}}\) is continuous in \([-1,1]\). Its derivative \[f'(x)=\frac{-2x}{2\sqrt{1-x^{2}}}=\frac{x}{\sqrt{1-x^{2}}},\] exists everywhere in this interval except at the endpoints \(x=\pm1\), but the fact that \(f\) is not differentiable at the endpoints does not violate the conditions of Rolle’s rule. In fact, we find \(f'(0)=0\) (also, see Figure 8).
A Physical Interpretation
Consider a train that moves on a straight railroad. If we see the train in a train station at 10 am and see the same train in the same station at 4 pm, we know that at some point, its speed was zero, because if the train never left the station, its speed was zero all the time between 10 am to 4 pm, and if it left the station and came back, it had first to stop, even for a second, to change its direction and come back. This is exactly what Rolle’s theorem states.
An important usage of Rolle’s theorem is in proving the Mean-Value Theorem that will be discussed in the next section.