To expand algebraic expressions, we need to use the distributive property. The reverse of expansion, called factorization or factoring, consists of using the distributive property in reverse and writing the expression as product of simpler ones. For example, we can write
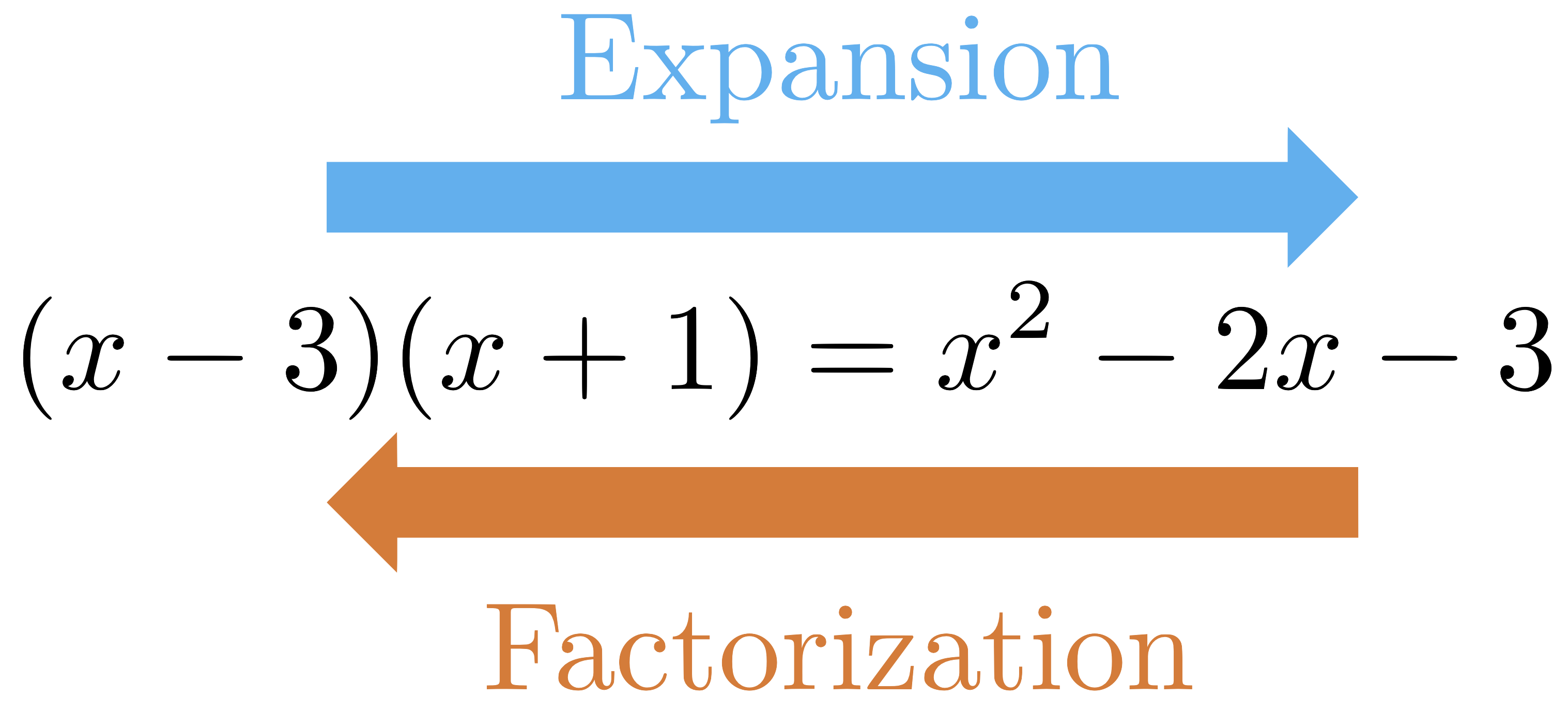
We say that $x-3$ and $x+1$ are factors of $x^{2}-2x-3$.
Click here to read why factorization is important
Collapse importance of factorization
Factorization has many applications. Here are a number of them.
Solving equations: If we can put an equation in a factored form $P\cdot Q=0$ (where $P$ and $Q$ are two expressions), then solving the problem reduces to solving two independent and often simpler equations $P=0$ and $Q=0$. (Recall if $ab=0$ then $a=0$ or $b=0$). For example instead of solving
\[x^{2}-2x-3=0\]
because $x^{2}-2x-3=(x-3)(x+1)$, we can solve
\[x-3=0\quad\text{or}\quad x+1=0\]
which shows at once
\[x=3\quad\text{or}\quad x=-1.\]
Similarly because
\[x^{3}-8x^{2}+17x-10=(x-1)(x-2)(x-5)\]
we immediately conclude
\[x^{3}-8x^{2}+17x-10=0\Rightarrow x=1\quad\text{or}\quad x=2\quad\text{or}\quad x=5.\]
Evaluating expressions: It is often easier to evaluate polynomials in the factored form. For example, evaluating $x^{3}-8x^{2}+17x-10$ reduces to only three subtractions and two multiplications if we use its factored form $(x-1)(x-2)(x-5)$.
Determining sign of the output: Sometimes, we need to find out for which values of the variable (often denoted by $x$) a polynomail is positive and for which values it is negative. Doing so is often much easier if we use the factored forms.
Simplifying rational expressions: Another application of factorization can be simplification of rational expressions. For example, $(x^{2}-1)/(x^{2}-2x-3)$ can be simplified as \[\frac{x^{2}-1}{x^{3}-2x-3}=\frac{(x-1)\cancel{(x+1)}}{(x-3)\cancel{(x+1)}}=\frac{x-1}{x-3}\qquad(x\neq-1)\]
However, factorization is not always possible and when it is possible, it does not necessarily yield simpler factors. For example, $x^{5}-32$ can be factored into $x-2$ and $x^{4}+2x^{3}+4x^{2}+8x+16$, but obviously we would rather solve $x^{5}-32=x^{5}-2^{5}=0$ than solve the following two equations
\[x-2=0,\quad x^{4}+2x^{3}+4x^{2}+8x+16=0.\]
Now let’s review some techniques of factorization.
Table of Contents
Common Factors
When there is a factor common to every term of an expression, we can simply factor it out by applying the distributive property in reverse.
Factorization of polynomials of the form x2 + bx + c
Because
\[(x+p)(x+q)=x^{2}+(p+q)x+pq\]
we can factor polynomials of the form $x^{2}+bx+c$ if we can find numbers $p$ and $q$ such that
\[p+q=b\quad\text{and}\quad pq=c.\]
In this section, we choose $p$ and $q$ by trial and error, but technically we can choose them systematically (see the Section on Solutions and Roots).
Special Factorization Formulas
If there is no common factor, to factor algebraic expressions we can sometimes use the following formulas that we reviewed in Section 1.12 and reverse the process.
| 1. $A^{2}-B^{2}=(A+B)(A-B)$ | (Difference of Squares) |
| 2. $A^{2}\pm2AB+B^{2}=(A\pm B)^{2}$ | (Perfect Square) |
| 3. $A^{3}-B^{3}=(A-B)(A^{2}+AB+B^{2})$ | (Difference of Cubes) |
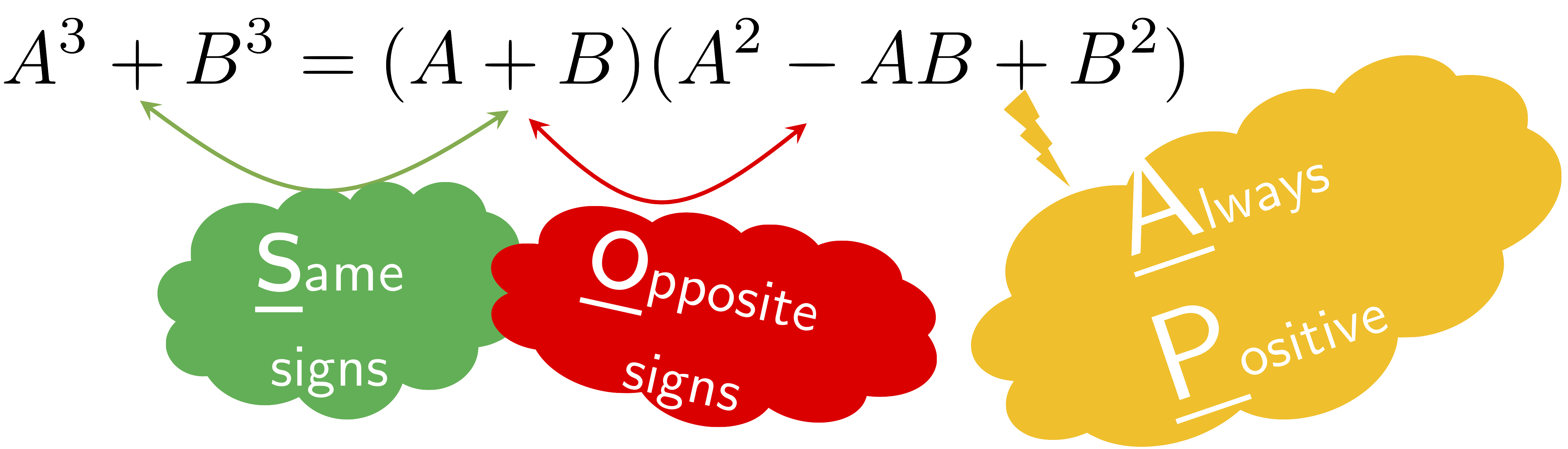
| 4. $A^{3}+B^{3}=(A+B)(A^{2}-AB+B^{2})$ | (Sum of Cubes) |
Mnemonics for Memorizing the Sum/Difference of Cubes Formulas:
Remember a cube of SOAP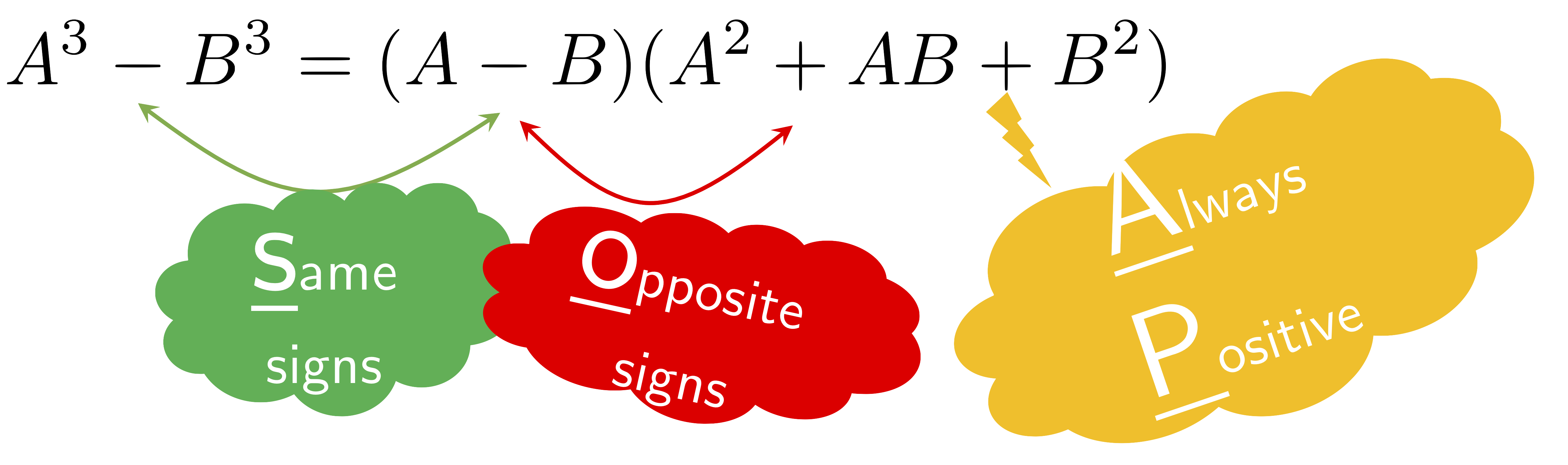
Click here for more special factorization formulas
Collapse more formulas
In general we can factor the sum or difference of two $n$th power ($n$ an integer) as follows
Difference, even exponent:
$A^{2n}-B^{2n}=(A^{n}-B^{n})(A^{n}+B^{n})$
Difference, even or odd exponent:
$A^{n}-B^{n}=(A-B)(A^{n-1}+A^{n-2}B+A^{n-3}B^{2}+\cdots+AB^{n-2}+B^{n-1})$
If we replace $B$ with $-B$ in the above formula and $n$ is odd then we will get the following formula (Note that if $n$ is even, we won’t get a new formula).
Sum, odd exponent:
$A^{n}+B^{n}=(A+B)(A^{n-1}-A^{n-2}B+A^{n-3}B^{2}-\cdots-AB^{n-2}+B^{n-1})$
Sum, even exponent:
$A^{n}+B^{n}$ cannot, in general, be factored.
Factorization by Grouping Terms
Sometimes there is no a common factor (other than $\pm1$) to all terms of a polynomial. However, the polynomial can sometimes be factored if we suitably group the terms that have common factors. This strategy may work for polynomials with at least four terms.
For example, we can factor the polynomial $x^{3}+3x^{2}+4x+12$ if we group the first two terms together and the last two terms together and then factor each group, namely
\begin{align*}
x^{3}+3x^{2}+4x+12 & =(x^{3}+3x^{2})+(4x+12)\\
& =x^{2}(x+3)+4(x+3)\\
& =(x+3)(x^{2}+4)
\end{align*}
For the last equation, we have factored out the common factor $x+3$.