Previously, we defined the concept of a local maximum and a local minimum. We showed that if \(f(c)\) is a local maximum or local minimum, then \(x=c\) is a critical number; that is, \(f'(c)=0\) or \(f'(c)\) does not exist. However, we did not discuss how to determine if \(f(c)\) is a local maximum, a local minimum, or neither. In this section, we provide a method for that.
Before we start, recall that if \(f'(x)>0\) on an interval, then \(f\) is an increasing function on that interval, and if \(f'(x)<0\), then \(f\) is a decreasing function (see this section).
- As we move along the curve of a function from left to right, if the sign of the derivative changes from \(+\) to \(-\) because the function changes from increasing \(\nearrow\) to decreasing \(\searrow\), the function has a local (or relative) maximum at the critical point (see Figure 1).
- As we move along the curve from left to right, if the sign of the derivative changes from \(-\) to \(+\) because the function changes from decreasing \(\searrow\) to increasing \(\nearrow\), the function has a local (or relative) minimum at the critical point (see Figure 2).
- As we move along the curve from left to right, if the sign of the derivative on the left and on the right of a critical point is the same, the function has no local maximum or minimum at the critical point (see Figure 3).
More precisely, we have the following theorem.
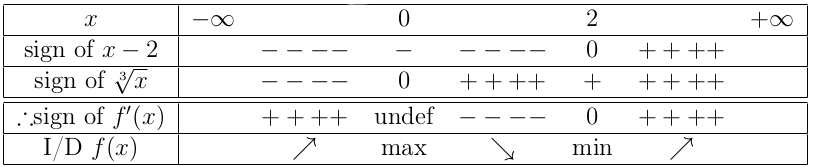
Theorem 1. (First Derivative Test) Assume \(f\) is continuous at the critical point \(c\).
(a) If \(f’\) is \(+\) to the left of \(c\) and is \(-\) to the right of \(c\), then \(f\) has a local maximum at \(c\).
(b) If \(f’\) is \(-\) to the left of \(c\) and is \(+\)to the right of \(c\), then \(f\) has local minimum at \(c\).
(c) If the sign of \(f’\) is the same to the right and left of \(c\), then \(f\) does NOT have a local extremum at \(c\).
- To remember the First Derivative Test, visualize \(\nearrow\searrow\) for the case where \(f’\) varies from \(+\) to \(-\) and \(\searrow\nearrow\) for the case where \(f’\) varies from \(-\) to \(+\).
- Recall that the critical points are the only possible candidates for local extrema.
To determine the sign of the derivative at points near a particular critical point, an alternative method to the sign table is to first substitute a value of the variable a little less than the corresponding critical point into the derivative formula, and then one a little greater.